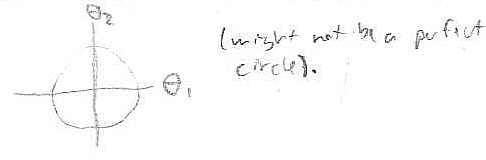0708-1300/Class notes for Thursday, September 20
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dror's Note
Come to my talk today at 4:30PM at the Fields Institute!
Class Notes
The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.
PDF file of the class notes typed up in latex can be located here
Tex version of the file is also avaliable here so that people can easily make changes and repost here if they wish.
Exercise
The solution(s) below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.
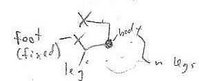
Configurations of a Generalized Cockroach (not entirely rigourous)
Let [math]\displaystyle{ C_n }[/math] be the manifold of configurations of a "cockroach" with [math]\displaystyle{ n }[/math] legs:
Q: What is [math]\displaystyle{ C_n }[/math]? In particular, what is [math]\displaystyle{ C_6 }[/math]?
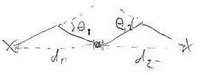
p[math]\displaystyle{ n=2 }[/math]: Consider [math]\displaystyle{ C_2 }[/math].
As in the picture, label the angles of the joints [math]\displaystyle{ \theta_1 }[/math] and [math]\displaystyle{ \theta_2 }[/math] and the distances from the body to the feet [math]\displaystyle{ d_1 }[/math] and [math]\displaystyle{ d_2 }[/math] respectively.
The value of [math]\displaystyle{ \theta_i }[/math] determines the value of [math]\displaystyle{ d_i }[/math]. So, given values [math]\displaystyle{ (\theta_1, \theta_2) }[/math], possible configurations are given by positions of the body, which must have distance [math]\displaystyle{ d_i }[/math] from the [math]\displaystyle{ i }[/math]th foot.
That is, the body must lie on the intersection of the two circles of radius [math]\displaystyle{ d_i }[/math] centred at the [math]\displaystyle{ i }[/math]th foot:
There are [math]\displaystyle{ 0, 1, }[/math] or [math]\displaystyle{ 2 }[/math] solutions for the body position.
If we look only at the top body position, the pair [math]\displaystyle{ (\theta_1, \theta_2) }[/math] determines a unique configuration.
So, we can plot the subset on [math]\displaystyle{ \R^2_{(\theta_1,\theta_2)} }[/math]:
The boundary points are where the "top" solution is in fact the unique solution.
By symmetry, taking the bottom solution gives us a similar region, and since the boundaries are where the top and bottom solutions coincide (there is only one solution along the boundary), the entire manifold is given by gluing the boundaries together. This gives a sphere.
[math]\displaystyle{ n=3 }[/math]: Configurations with [math]\displaystyle{ 3 }[/math] legs consist of a configuration with [math]\displaystyle{ 2 }[/math] legs plus the configuration of the third leg. The configuration of the first [math]\displaystyle{ 2 }[/math] legs fixes the position of the body - and thus, the distance [math]\displaystyle{ d_3 }[/math] from the third foot to the body.
For certain configurations of the first two legs, the body is too far from the third foot, so these are not found as part of configurations with three feet. When the distance from the body to the third foot equals the length of the third leg completely extended, this gives a unique configuration of the [math]\displaystyle{ 3 }[/math]-legged cockroach. Any closer and there are two possible configurations, corresponding to the two ways that the third joint can bend.
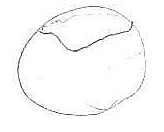
Let [math]\displaystyle{ R }[/math] be the region in [math]\displaystyle{ C_2 = S_2 }[/math] where the distance to the third leg is close enough to give solutions. The boundary of [math]\displaystyle{ R }[/math] is a curve, consisting of all the points at which there is a unique solution:
So the manifold [math]\displaystyle{ C_3 }[/math] is given by taking two copies of [math]\displaystyle{ R }[/math] and gluing their boundaries together. This gives a sphere.
[math]\displaystyle{ n \geq 3 }[/math]: Likewise, given that [math]\displaystyle{ C_n = S_2 }[/math], it follows that [math]\displaystyle{ C_{n+1} = S_2 }[/math] also. In particular, [math]\displaystyle{ C_6 = S_2 }[/math].
Dror's Evaluation
The solution for [math]\displaystyle{ n=2 }[/math] seems right but hard to understand. For [math]\displaystyle{ n=3 }[/math] the solution is absolutely right. Unfortunately for [math]\displaystyle{ n\gt 3 }[/math] the solution is wrong. (Why?)
--Drorbn 19:46, 24 September 2007 (EDT)
another solution for n<5
Here's a not-too-sketchy solution for n=3 and a sketch of how the same approach works for n=4. The strategy also works for a 2-legged roach but I really really can't do 5 or more. Perhaps someone else can help! Note that for n=4 we have a torus, not a sphere! p.s. Sorry if the image is upside-down or hard to get to, I am just learning how to deal with technology