0708-1300/Class notes for Tuesday, February 5
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
On Term Exam 2
Term Exam 2 will take place on Monday February 11, 2008, in room GB217 of the Galbraith Building (across St. George from Bahen), starting at 6:10PM sharp and ending at 8PM. The material is everything since the last exam - differential forms and Stokes' theorem from last semester, and the fundamental group and covering spaces from this semester. The general style and form of the exam will be exactly the same as the style and form of Term Exam 1, though it may be a bit harder.
Imprecise Definition. "Sketch the proof of a major theorem" means that you should write an outline of the proof, omitting details that any graduate student taking this class could have considered as exercises while studying the proof for the first time, while not omitting anything that really requires creative thinking.
Example. A sketch of the proof that every smooth manifold carries a proper smooth function into the positive reals would be "let be a partition of unity subordinate to a cover of by open sets with compact closures, and take ". The formula in the quoted statement above requires creativity and is hard to come by; so every sketch must contain it or something equivalent to it. The proof that the resulting function is indeed smooth and proper is an exercise and may well be omitted.
Unbased Covering Spaces
Let be a topological space and let be the category of covering spaces of : The category whose objects are (unbased!) coverings and whose morphisms are maps between such coverings that commute with the covering projections - a morphism between and is a map so that the diagram below is commutative:
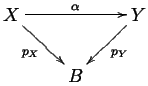
|
Every topologists' highest hope is to find that her/his favourite category of topological objects is equivalent to some category of easily understood algebraic objects. The following theorem realizes this dream in full in the case of the category of covering spaces of any reasonable base space :
Theorem 1. (Classification of covering spaces)
- If has base point and fundamental group , then the map which assigns to every covering its fiber over the basepoint induces a functor from the category of coverings of to the category of -sets - sets with a right -action and set maps that respect the action.
- If in addition is connected, locally connected and semi-locally simply connected then the functor is an equivalence of categories. (In fact, this is iff).
If indeed the categories and are equivalent, one should be able to extract everything topological about a covering from its associated -set . The following theorem shows this to be right in at least two ways:
Theorem 2. For connected, locally connected and semi-locally simply connected and a covering of :
- The set of connected components of is in a bijective correspondence with the set of orbits of in .
- Let be a basepoint for that covers the basepoint of . Then the fundamental group is isomorphic via the projection into to the stabilizer group of in .
(Both assertions of this theorem can be sharpened to deal with morphisms as well, but we will not bother to do so).
Based Covering Spaces
There are similar theorems (call them theorem 1' and theorem 2') relating the category of based covering spaces with the category of based -sets.
The Main Point
Ok. Every math technician can spend some time and effort and understand the statements and (only then) the proofs of these two theorems. Your true challenge is to digest the following statement:
| All there is to know about covering spaces follows from these two theorems |
In particular, the following facts are all simple algebraic corollaries of these theorems:
Corollary 1. If is connected then its covering number (="number of decks") is equal to the index of in , and the decks of are in a non-canonical correspondence with the left cosets of in .
Corollary 2. If is semi-locally simply connected, there exists a unique (up to base-point-preserving isomorphism) "universal covering space of " (a connected and simply connected covering ).
Corollary 3. The group of automorphisms of the universal covering is equal to .
Corollary 4. .
Corollary 5. .
Corollary 6. If is semi-locally simply connected, then for every there is a unique (up to base-point-preserving isomorphism) connected covering space with .
Corollary 7. If for are connected coverings of with groups and if then is a covering of of covering number .
Corollary 8. If is semi-locally simply connected there is a bijection between conjugacy classes of subgroups of and unbased connected coverings of .
Corollary 9. A connected covering is normal (for any theres an automorphism of with ) iff its group is normal in .
Corollary 10. If is a connected covering of and , then where is the normalizer of in .
Proposition 11. If we forgot anything, it follows too.
Steps in the proofs of Theorem 1 and 2
- Use path liftings to construct a right action of on .
- Show that this is indeed a group action and that morphisms of coverings induce morphisms of right -sets.
- Start the construction of an "inverse" functor of : Use spelunking (cave exploration) to construct a universal covering of , if is semi-locally simply connected.
- Show that .
- Use the construction of or the general lifting property for covering spaces to show that there is a left action of on .
- For a general right -set set and show that is a covering of and .
- Show that is compatible with maps between right -sets.
- Understand the relationship between connected components and orbits.
- Prove Theorem 2.
- Use the existence and uniqueness of lifts to show that is equivalent to the identity functor (working connected component by connected component).
A Deep Thought Question
What does it at all mean " is equivalent to the identity functor" (and first, why can't it simply be the identity functor)? And even harder, what does it at all mean for two categories to be "equivalent"? If you answer this question correctly, you'll probably re-invent the notions of "natural transformation between two functors" and "natural equivalence", that gave the historical impetus for the development of category theory.
From the Wikipedia entry for Natural Transformation:
Saunders Mac Lane, one of the founders of category theory, is said to have remarked, "I didn't invent categories to study functors; I invented them to study natural transformations." Just as the study of groups is not complete without a study of homomorphisms, so the study of categories is not complete without the study of functors. The reason for Mac Lane's comment is that the study of functors is itself not complete without the study of natural transformations.
The context of Mac Lane's remark was the axiomatic theory of homology. Different ways of constructing homology could be shown to coincide: for example in the case of a simplicial complex the groups defined directly, and those of the singular theory, would be isomorphic. What cannot easily be expressed without the language of natural transformations is how homology groups are compatible with morphisms between objects, and how two equivalent homology theories not only have the same homology groups, but also the same morphisms between those groups.
























































