0708-1300/Class notes for Tuesday, February 12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
INCOMPLETE typed notes at bottom
Class Notes
The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.
Typed Notes
Informal definition of homology:
Given X (General topological spaces with no base point) then H_n(X) = {Boundaryless compact n-dim m submanifolds of X}/{Boundaries of (n+1)-dim submanifolds
because , the this makes sense.
We will need to formalize this by using vector spaces generated by sets.
We begin by computing the homology of some examples. These are correct in spirit but very wrong in the details, indeed, we havn't even defined what the right details are!
Now, 0 dimensional submanifolds are merely points. 1 dimensional submanifolds are paths. So, if two points have a path between them, then the points contribute nothing to the zeroth homology. Hence H_0(S^1) = H_0(S^2) = 0 etc...
Hence, H_0(connected) = <pts>/{all points are connected] = \mathbb{Z}
H_1(S^1) = \mathbb{Z} as boundaryless paths are generated by loops around the circle, which are vacuously not the boundary of 2 manifolds.
H_1(S^2) = <closed paths>/<boundaries of disks > = 0
/ nothing =
In general we have
Likewise, we know the zeroth and second homology of the torus is \mathbb{Z}
We now need to compute the first homology of the torus. That is, we search for closed paths with no inner disk.
We think of the torus generated by a square subset of the real plane with the usual identifications. Call one side a and the other b. Now consider a diagonal across the square, labeled c. Clearly we have a path with, c = a + b, which is the boundary of a triangle.
Varying the diagonal into an arbitrary path which yields the same result we see that H_1(T^2)=\mathbb{Z}^2
We get functorality as for f:X\rightarrow Y we get a map f^*:H_n(X)\rightarrow H_n(Y) as f maps boundaryless manifolds to boundaryless manifolds.
Applications
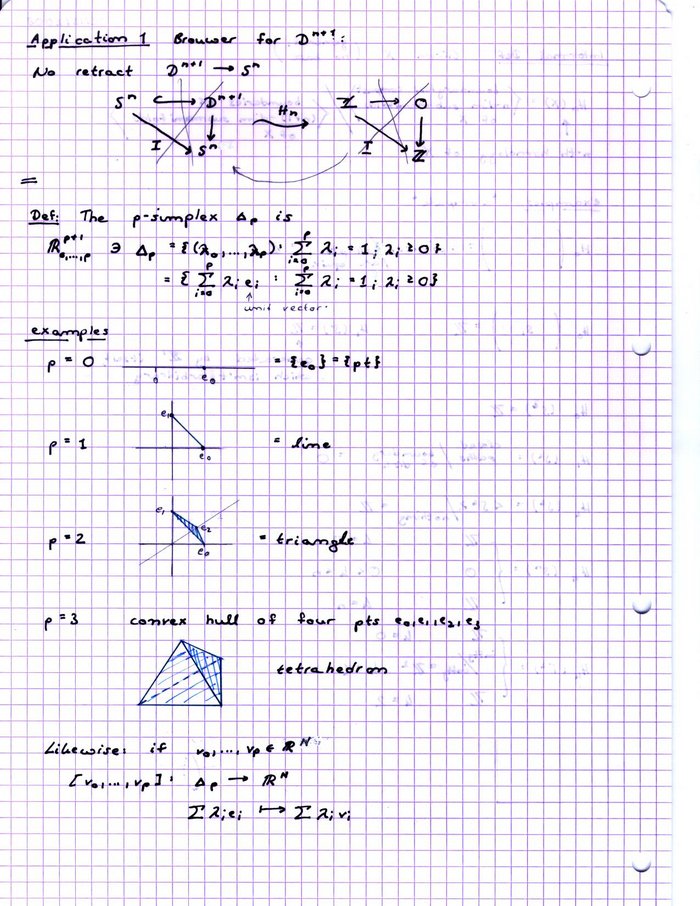
Brouwer's theorem for D^{n+1}
I.e., there is no retract D^{n+1}\rightarrow S^n
Indeed, if there were such an retract we would get a commuting diagram and I = i :S^n\rightarrow S^n} where I is the identity on S^n and i is the natural inclusion into D^{n+1}. But after applying the functor this would get a commuting diagram where S^n goes to \mathbb{Z} and D^{n+1} goes to zero. But then have I* = 0 map, this is impossible.
Definition:
The p-simplex \Delta_p is is
\mathbb{R}^{p+1}\ni\Delta_p:=\{(\lambda_0\cdots\lambda_p)\ |\ \sum_i^p \lambda_i = 1,\ \lambda_i\geq0\} = \{\sum\lambda_i e_i\ |\ \sum_i^p \lambda_i = 1,\ \lambda_i\geq0\}
Example
p=0 is just the point 1 on the real line.
p=1 is the diagonal line between (1,0) and (0,1) in the real plane. here e_1 represents the vector from 0 to (0,1) and e_0 represents the vector from 0 to (1,0)
p=2 forms a triangle between the tips of the three unit vectors in \mathbb{R}^3.
In general, we have the convex full of p+1 points.
Likewise, if (v_0,\cdots, v_p)\in\mathbb{R}^N then have map [v_0,\cdots, v_p]:\Delta_p\rightarrow\mathbb{R}^N defined by \sum\lambda_i e_i\mapsto \sum \lambda_i v_i
Now, we want to define the boundary of a simplex. Loosely, we get a bunch of p-1 simplexes found by forgetting a vertex each time.
Definition
F_i^p:\Delta_{p-1}\rightarrow\Delta_p is the ith face of \Delta_p, namely, F_i^p = [e_0\cdots \hat{e_i}\cdots e_p]
Definition
Given X, \Delta_p(X)=C_p(X) = <p\ simplexes\ in\ X> = \{\sum a_i\sigma_i\ |\ a_i\in\mathbb{Z},\ \sigma_i:\Delta_p\rightarrow X\ is\ cont.\}
Note: \sigma is not necessarily 1:1 as was implied in the earlier naive computations. Furthermore, we note that C_p(X) has an abelian group structure)
Definition: \partial_p:C_p(X)\rightarrow Cc_{p-1}(X) a group homomorphism via \sum a_i\sigma_i\mapsto \sum a_i\partial_p(\sigma_i) where \partial_p\sigma = \sum_{i=0}^p (-1)^i\sigma\circ\F_i^p
This results in a chain \cdots C_3(X)\rightarrow^{\partial_3}C_2(X)\rightarrow^{\partial_2}C_1(X)\rightarrow^{\partial_1}C_0(X)
Definition
Z_p(X) = ker\partial_p called "p cycles in X"
B_p(X) = Im\partial_{p+1} called "p boundaries in X"
We want to define H_p(X) = Z_p(X)/B_p(X)
Lemma
B_p(X)\subset Z_p(X) \Leftrightarrow im\partial{p+1}\subset \partial_p\Leftrightarrow \partial_p\circ\partial_{p+1} =0
Notationally we simply write \partial^2 = 0
Let \sigma\in C_{p+1}
\sigma:\Delta_{p+1}\rightarrow X, \partial\sigma = \sum_{i=0}^p (-1)^i\sigma\circ F_i^{p}
\partial\partial\sigma = \partial(\sum (-1)^i\sigma\circ F_i^p) = \sum_{i=0}^{p+1}\sum_{j=0}^p\sigma\circ F_i^p\circ F_j^{p-1}(-1)^{i+j}
I.e., dropping e_m, e_n occurs twice, only with a different sign. Formally,
F_i^p\circ F_j^{p-1} = [e_o\cdots \hat{e_j},\hat{e_i}\cdots e_{p+1}] for i>j and
F_i^p\circ F_j^{p-1} = [e_o\cdots \hat{e_i},\hat{e_j+1}\cdots e_{p+1}] for i\leq j
So \partial\partial\sigma = \sum_{i=o}^{p+1}\sum_{j=0}^{p-1}(-1)^{i+j}\sigma\circ[\hat{e_j}\hat{e_i}] + \sum_{i=0}^{p+1}\sum_{j=i}^p (-1)^{i+j}\sigma\circ[\hat{e_i}\hat{e_{j+1}}]