0708-1300/Homework Assignment 6

0708-1300/Navigation Panel   Add your name / see who's in! # Week of... Links Fall Semester 1 Sep 10 About, Tue, Thu 2 Sep 17 Tue, HW1, Thu 3 Sep 24 Tue, Photo, Thu 4 Oct 1 Questionnaire, Tue, HW2, Thu 5 Oct 8 Thanksgiving, Tue, Thu 6 Oct 15 Tue, HW3, Thu 7 Oct 22 Tue, Thu 8 Oct 29 Tue, HW4, Thu, Hilbert sphere 9 Nov 5 Tue,Thu, TE1 10 Nov 12 Tue, Thu 11 Nov 19 Tue, Thu, HW5 12 Nov 26 Tue, Thu 13 Dec 3 Tue, Thu, HW6 Spring Semester 14 Jan 7 Tue, Thu, HW7 15 Jan 14 Tue, Thu 16 Jan 21 Tue, Thu, HW8 17 Jan 28 Tue, Thu 18 Feb 4 Tue 19 Feb 11 TE2, Tue, HW9, Thu, Feb 17: last chance to drop class R Feb 18 Reading week 20 Feb 25 Tue, Thu, HW10 21 Mar 3 Tue, Thu 22 Mar 10 Tue, Thu, HW11 23 Mar 17 Tue, Thu 24 Mar 24 Tue, HW12, Thu 25 Mar 31 Referendum,Tue, Thu 26 Apr 7 Tue, Thu R Apr 14 Office hours R Apr 21 Office hours F Apr 28 Office hours, Final (Fri, May 2) Register of Good Deeds Errata to Bredon's Book

Announcements go here

Reading

At your leisure, read your class notes over the break, and especially at some point right before classes resume next semester. Here are a few questions you can ask yourself while reading:

• Do you understand pullbacks of differential forms?
• Do you think you could in practice integrate any differential form on any manifold (at least when the formulas involved are not too messy)?
• Do you understand orientations and boundaries and how they interact?
• Why is Stokes' theorem true? Both in terms of the local meaning of $d$, and in terms of a formal proof.
• Do you understand the two and three dimensional cases of Stokes' theorem?
• Do you understand the Hodge star operator $\star$?
• How did we get $d\star dA=J$ from the least action principle?
• Do you understand how Poincare's lemma entered the derivation of Maxewell's equations?
• Do you understand the operator $P$? (How was it used, formally derived, and what is the intuitive picture behind it?)
• What was $H_{dR}$ and how did it relate to pullbacks and homotopy.

Doing

Solve the following problems and submit your solutions of problems 1, 3 and 4. This is a very challenging collection of problems; I expect most of you to do problem 2 with no difficulty (it is a repeat of an older problem), problem 1 with some effort, and I hope each of you will be able to do at least one further problem. It will be great if some of you will do all problems!

Problem 1. If $M$ is a compact orientable $n$-manifold with no boundary, show that $H_{dR}^{n}(M)\neq 0$.

Problem 2. The standard volume form on $S^{2}$ is the form $\omega$ given by $\omega ={\frac {1}{4\pi }}\left(xdy\wedge dz+ydz\wedge dx+zdx\wedge dy\right)$. Show that $\int _{S^{2}}\omega =1$.

Problem 3. Show that if $\omega \in \Omega ^{2}(S^{2})$ satisfies $\int _{S_{2}}\omega =0$, then $\omega$ is exact. Deduce that if $w_{1}\in \Omega ^{2}(S^{2})$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_2\in\Omega^2(S^2)} satisfy $\int _{S_{2}}\omega _{1}=\int _{S_{2}}\omega _{2}$, then $[\omega _{1}]=[\omega _{2}]$ as elements of $H_{dR}^{2}(S^{2})$. Deduce further that $\dim H_{dR}^{2}(S^{2})=1$.

Problem 4. A "link" in ${\mathbb {R} }^{3}$ is an ordered pair $\gamma =(\gamma _{1},\gamma _{2})$, in which $\gamma _{1}$ and $\gamma _{2}$ are smooth embeddings of the circle $S^{1}$ into ${\mathbb {R} }^{3}$, whose images (called "the components of $\gamma$") are disjoint. Two such links are called "isotopic", if one can be deformed to the other via a smooth homotopy along which the components remain embeddings and remain disjoint. Given a link $\gamma$, define a map $\Phi _{\gamma }:S^{1}\times S^{1}\to S^{2}$ by $\Phi _{\gamma }(t_{1},t_{2}):={\frac {\gamma _{2}(t_{2})-\gamma _{1}(t_{1})}{||\gamma _{2}(t_{2})-\gamma _{1}(t_{1})||}}$. Finally, let $\omega$ be the standard volume form of $S^{2}$, and define "the linking number of $\gamma =(\gamma _{1},\gamma _{2})$" to be $l(\gamma )=l(\gamma _{1},\gamma _{2}):=\int _{S^{1}\times S^{1}}\Phi _{\gamma }^{\star }\omega$. Show

1. If two links $\gamma$ and $\gamma '$ are isotopic, then their linking numbers are the same: $l(\gamma )=l(\gamma ')$.
2. If $\omega '$ is a second 2-form on $S^{2}$ for which $\int _{S^{2}}\omega '=1$ and if $l'(\gamma )$ is defined in the same manner as $l(\gamma )$ except replacing $\omega$ with $\omega '$, then $l(\gamma )=l'(\gamma )$. (In particular this is true if $\omega '$ is very close to a $\delta$-function form at the north pole of $S^{2}$).
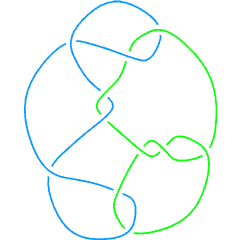
3. Compute (but just up to an overall sign) the linking number of the link L11a193, displayed below:

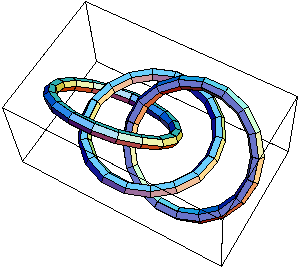
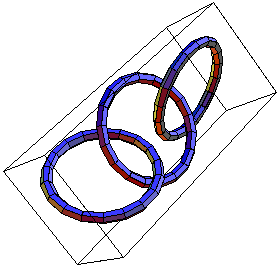
The links L11a193, $\gamma _{3}$ and $\gamma '_{3}$.

Just for Fun

Prove that the two (3-component) links $\gamma _{3}$ and $\gamma '_{3}$ shown above are not isotopic, yet their complements are diffeomorphic. (See more at Classes: 2004-05: Math 1300Y - Topology: Homework Assignment 5)

Due Date

This assignment is due in class on Thursday January 10, 2007.