0708-1300/Homework Assignment 6
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The information below is preliminary and cannot be trusted! (v)
Reading
At your leisure, read your class notes over the break, and especially at some point right before classes resume after the break.
Doing
Solve the following problems and submit your solutions of problems 1, 3 and 4. This is a very challenging collection of problems; I expect most of you to do problem 2 with no difficulty (it is a repeat of an older problem), problem 1 with not too much difficulty, and I hope each of you will be able to do at least one further problem. It will be great if some of you will do all problems!
Problem 1. If [math]\displaystyle{ M }[/math] is a compact orientable [math]\displaystyle{ n }[/math]-manifold with no boundary, show that [math]\displaystyle{ H^n_{dR}(M)\neq 0 }[/math].
Problem 2. The standard volume form on [math]\displaystyle{ S^2 }[/math] is the form [math]\displaystyle{ \omega }[/math] given by [math]\displaystyle{ \omega=\frac{1}{4\pi}\left(xdy\wedge dz+ydz\wedge dx+zdx\wedge dy\right) }[/math]. Show that [math]\displaystyle{ \int_{S^2}\omega=1 }[/math].
Problem 3. Show that if [math]\displaystyle{ \omega\in\Omega^2(S^2) }[/math] satisfies [math]\displaystyle{ \int_{S_2}\omega=0 }[/math], then [math]\displaystyle{ \omega }[/math] is exact, and therefore, if [math]\displaystyle{ w_1\in\Omega^2(S^2) }[/math] and [math]\displaystyle{ w_2\in\Omega^2(S^2) }[/math] satisfy [math]\displaystyle{ \int_{S_2}\omega_1=\int_{S_2}\omega_2 }[/math], then [math]\displaystyle{ [\omega_1]=[\omega_2] }[/math] as elements of [math]\displaystyle{ H^2_{dR}(S^2) }[/math].
Problem 4. A "link" in [math]\displaystyle{ {\mathbb R}^3 }[/math] is an ordered pair [math]\displaystyle{ \gamma=(\gamma_1, \gamma_2) }[/math], in which [math]\displaystyle{ \gamma_1 }[/math] and [math]\displaystyle{ \gamma_2 }[/math] are smooth embeddings of the circle [math]\displaystyle{ S^1 }[/math] into [math]\displaystyle{ {\mathbb R}^3 }[/math], whose images (called "the components of [math]\displaystyle{ \gamma }[/math]") are disjoint. Two such links are called "isotopic", if one can be deformed to the other via a smooth homotopy along which the components remain embeddings and remain disjoint. Given a link [math]\displaystyle{ \gamma }[/math], define a map [math]\displaystyle{ \Phi_\gamma:S^1\times S^1\to S^2 }[/math] by [math]\displaystyle{ \Phi_\gamma(t_1,t_2):=\frac{\gamma_2(t_2)-\gamma_1(t_1)}{||\gamma_2(t_2)-\gamma_1(t_1)||} }[/math]. Finally, let [math]\displaystyle{ \omega }[/math] be the standard volume form of [math]\displaystyle{ S^2 }[/math], and define "the linking number of [math]\displaystyle{ \gamma=(\gamma_1, \gamma_2) }[/math]" to be [math]\displaystyle{ l(\gamma)=l(\gamma_1,\gamma_2):=\int_{S^1\times S^1}\Phi_\gamma^\star\omega }[/math]. Show
- If two links [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ \gamma' }[/math] are isotopic, then their linking numbers are the same: [math]\displaystyle{ l(\gamma)=l(\gamma') }[/math].
- If [math]\displaystyle{ \omega' }[/math] is a second 2-form on [math]\displaystyle{ S^2 }[/math] for which [math]\displaystyle{ \int_{S^2}\omega'=1 }[/math] and if [math]\displaystyle{ l'(\gamma) }[/math] is defined in the same manner as [math]\displaystyle{ l(\gamma) }[/math] except replacing [math]\displaystyle{ \omega }[/math] with [math]\displaystyle{ \omega' }[/math], then [math]\displaystyle{ l(\gamma)=l'(\gamma) }[/math]. (In particular this is true if [math]\displaystyle{ \omega' }[/math] is very close to a [math]\displaystyle{ \delta }[/math]-function form at the north pole of [math]\displaystyle{ S^2 }[/math]).
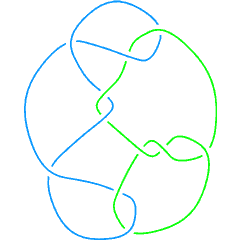
- Compute (but just up to an overall sign) the linking number of the link L11a193, displayed below:
|
|
|
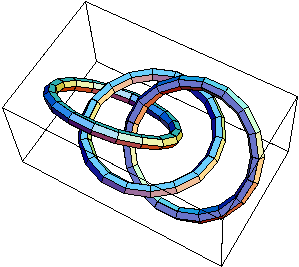
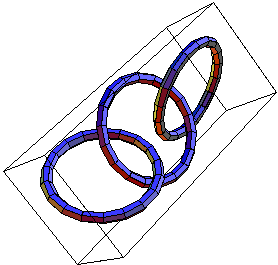
| The links L11a193, [math]\displaystyle{ \gamma_3 }[/math] and [math]\displaystyle{ \gamma'_3 }[/math]. | ||
Just for Fun
Prove that the two (3-component) links [math]\displaystyle{ \gamma_3 }[/math] and [math]\displaystyle{ \gamma'_3 }[/math] shown above are not isotopic, yet their complements are diffeomorphic. (See more at Classes: 2004-05: Math 1300Y - Topology: Homework Assignment 5)
Due Date
This assignment is due in class on Thursday January 10, 2007.
