0708-1300/Class notes for Tuesday, September 11
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In Small Scales, Everything's Linear
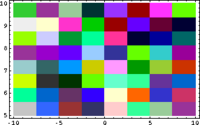
|
[math]\displaystyle{ \longrightarrow }[/math] | 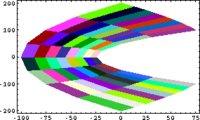
|
| [math]\displaystyle{ z }[/math] | [math]\displaystyle{ \mapsto }[/math] | [math]\displaystyle{ z^2 }[/math] |
Code in Mathematica:
QuiltPlot[{f_,g_}, {x_, xmin_, xmax_, nx_}, {y_, ymin_, ymax_, ny_}] :=
Module[
{dx, dy, grid, ix, iy},
SeedRandom[1];
dx=(xmax-xmin)/nx;
dy=(ymax-ymin)/ny;
grid = Table[
{x -> xmin+ix*dx, y -> ymin+iy*dy},
{ix, 0, nx}, {iy, 0, ny}
];
grid = Map[({f, g} /. #)&, grid, {2}];
Show[
Graphics[Table[
{
RGBColor[Random[], Random[], Random[]],
Polygon[{
grid[[ix, iy]],
grid[[ix+1, iy]],
grid[[ix+1, iy+1]],
grid[[ix, iy+1]]
}]
},
{ix, nx}, {iy, ny}
]],
Frame -> True
]
]
QuiltPlot[{x, y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
QuiltPlot[{x^2-y^2, 2*x*y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
See also 06-240/Linear Algebra - Why We Care.
Class Notes
The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.
Differentiability
Let [math]\displaystyle{ U }[/math], [math]\displaystyle{ V }[/math] and [math]\displaystyle{ W }[/math] be two normed finite dimensional vector spaces and let [math]\displaystyle{ f:V\rightarrow W }[/math] be a function defined on a neighborhood of the point [math]\displaystyle{ x }[/math].
Definition:
We say that [math]\displaystyle{ f }[/math] is differentiable (diffable) at [math]\displaystyle{ x }[/math] if there is a linear map [math]\displaystyle{ L }[/math] so that
[math]\displaystyle{ \lim_{h\rightarrow0}\frac{|f(x+h)-f(x)-L(h)|}{|h|}=0. }[/math]
In this case we will say that [math]\displaystyle{ L }[/math] is a differential of [math]\displaystyle{ f }[/math] at [math]\displaystyle{ x }[/math] and will denote it by [math]\displaystyle{ df_{x} }[/math].
Theorem
If [math]\displaystyle{ f:V\rightarrow W }[/math] and [math]\displaystyle{ g:U\rightarrow V }[/math] are diffable maps then the following assertions hold:
- [math]\displaystyle{ df_{x} }[/math] is unique.
- [math]\displaystyle{ d(f+g)_{x}=df_{x}+dg_{x} }[/math]
- If [math]\displaystyle{ f }[/math] is linear then [math]\displaystyle{ df_{x}=f }[/math]
- [math]\displaystyle{ d(f\circ g)_{x}=df_{g(x)}\cdot dg_{x} }[/math]
- For every scalar number [math]\displaystyle{ \alpha }[/math] it holds [math]\displaystyle{ d(\alpha f)_{x}=\alpha df_{x} }[/math]
Implicit Function Theorem
Example Although [math]\displaystyle{ x^2+y^2=1 }[/math] does not defines [math]\displaystyle{ y }[/math] as a function of [math]\displaystyle{ x }[/math], in a neighborhood of [math]\displaystyle{ (0;-1) }[/math] we can define [math]\displaystyle{ g(x)=-\sqrt{1-x^2} }[/math] so that [math]\displaystyle{ x^2+g(x)^2=1 }[/math]. Furthermore, [math]\displaystyle{ g }[/math] is differentiable with differential [math]\displaystyle{ dg_{x}=\frac{x}{\sqrt{1-x^2}} }[/math]. This is a motivation for the following theorem.
Notation
If [math]\displaystyle{ f:X\times Y\rightarrow Z }[/math] then given [math]\displaystyle{ x\in X }[/math] we will define [math]\displaystyle{ f_{[x]}:Y\rightarrow Z }[/math] by [math]\displaystyle{ f_{[x]}(y)=f(x;y). }[/math]
Definition
[math]\displaystyle{ C^{p}(V) }[/math] will be the class of all functions defined on [math]\displaystyle{ V }[/math] with continuous partial derivatives up to order [math]\displaystyle{ p. }[/math]
Theorem(Implicit function theorem)
Let [math]\displaystyle{ f:\mathbb{R}^n \times \mathbb{R}^m\rightarrow \mathbb{R}^m }[/math] be a [math]\displaystyle{ C^{1}(\mathbb{R}^n \times \mathbb{R}^m) }[/math] function defined on a neighborhood [math]\displaystyle{ U }[/math] of the point [math]\displaystyle{ (x_0;y_0) }[/math] and such that [math]\displaystyle{ f(x_0;y_0)=0 }[/math] and suppose that [math]\displaystyle{ d(f_{[x]})_{y} }[/math] is non-singular then, the following results holds:
There is an open neighborhood of [math]\displaystyle{ x_0 }[/math], [math]\displaystyle{ V\subset U }[/math], and a diffable function [math]\displaystyle{ g:V\rightarrow\mathbb{R}^m }[/math] such that [math]\displaystyle{ g(x_0)=y_0 }[/math] and for every [math]\displaystyle{ x\in V }[/math] [math]\displaystyle{ f(x;g(x))=0. }[/math].
