0708-1300/Class notes for Thursday, October 4
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Movie Time
With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's home, a talk I once gave, and the movie itself, on google video.
Class Notes
Definition
Let [math]\displaystyle{ \theta : M^m \rightarrow N^n\! }[/math] be a smooth map between manifolds. If for each [math]\displaystyle{ p \in M\! }[/math] the differential [math]\displaystyle{ d\theta_p : T_p M \rightarrow T_{\theta(p)} N\! }[/math] is surjective, [math]\displaystyle{ \theta\! }[/math] is called a submersion.
Theorem
If [math]\displaystyle{ \theta : M^m \rightarrow N^n\! }[/math] is a smooth map between manifolds and for some [math]\displaystyle{ p \in M\! }[/math] the differential [math]\displaystyle{ d\theta_p : T_p M \rightarrow T_{\theta(p)} N\! }[/math] is surjective then there exist charts [math]\displaystyle{ \phi : U \rightarrow U' \subset \mathbb{R}^m\! }[/math] and [math]\displaystyle{ \psi : V \rightarrow V' \subset \mathbb{R}^n\! }[/math] on [math]\displaystyle{ M\! }[/math] and [math]\displaystyle{ N\! }[/math] respectively such that
- [math]\displaystyle{ \phi(p) = 0\! }[/math]
- [math]\displaystyle{ \psi\left(\theta(p)\right) = 0\! }[/math]
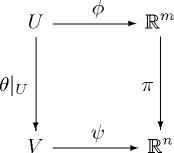
- The diagram
commutes, where [math]\displaystyle{ \pi : \mathbb{R}^m = \mathbb{R}^n \times \mathbb{R}^{m-n} \rightarrow \mathbb{R}^n\! }[/math] is the canonical projection.
Proof
Since translations are diffeomorphisms of [math]\displaystyle{ \mathbb{R}^k\! }[/math] for every [math]\displaystyle{ k \in \mathbb{N}\! }[/math], it is trivial to find charts [math]\displaystyle{ \phi_0 : U_0 \rightarrow U_0' \subset \mathbb{R}^m\! }[/math] and [math]\displaystyle{ \psi : V \rightarrow V' \subset \mathbb{R}^m\! }[/math] such that [math]\displaystyle{ \phi(p) = 0 \in \mathbb{R}^m\! }[/math] and [math]\displaystyle{ \psi(\theta(p)) = 0 \in \mathbb{R}^n\! }[/math]. Furthermore, since [math]\displaystyle{ V\! }[/math] is open, [math]\displaystyle{ U_0\! }[/math] is open and [math]\displaystyle{ \theta\! }[/math] is continuous, [math]\displaystyle{ U_0 \cap \theta^{-1}\left(V\right) \subset M\! }[/math] is open so that we may assume [math]\displaystyle{ U_0 \subset \theta^{-1}\left(V\right)\! }[/math] without loss of generality.
Let [math]\displaystyle{ \theta_0 = \psi \circ \theta \circ \phi_0^{-1} : U_0' \rightarrow V'\! }[/math] be the local representative of [math]\displaystyle{ \theta\! }[/math] and let [math]\displaystyle{ D_0 : \mathbb{R}^m \rightarrow \mathbb{R}^n \! }[/math] be the local representative of [math]\displaystyle{ d\theta_p\! }[/math]. Since [math]\displaystyle{ d\theta_p\! }[/math] is onto, we may apply a change of basis [math]\displaystyle{ T : \mathbb{R}^m \rightarrow \mathbb{R}^m }[/math] such that [math]\displaystyle{ D_0 = T^{-1} \circ \pi \circ T }[/math].
Let [math]\displaystyle{ \phi_1 = T \circ \phi_0\! }[/math]. Then [math]\displaystyle{ \phi_1\! }[/math] is a chart because [math]\displaystyle{ T\! }[/math] is a diffeomorphism. Let [math]\displaystyle{ \theta_1 = \psi \circ \theta \circ \phi_1^{-1} : U_0' \rightarrow V'\! }[/math] be the corresponding local representative, define [math]\displaystyle{ \zeta : U_0' \rightarrow \mathbb{R}^m\! }[/math] by [math]\displaystyle{ \zeta(x,y) = (\theta_1(x,y),y)\! }[/math], and let [math]\displaystyle{ D_1 : \mathbb{R}^m \rightarrow \mathbb{R}^n\! }[/math] be the differential of [math]\displaystyle{ \theta_1\! }[/math] at [math]\displaystyle{ 0\! }[/math]. Then, by construction of [math]\displaystyle{ T\! }[/math] we have that [math]\displaystyle{ D_1 = \pi\! }[/math] and hence [math]\displaystyle{ d \zeta_0 = \mathrm{id}_{\mathbb{R}^m}\! }[/math], which is invertible. Hence, the inverse function gives the existence of non-empty open set [math]\displaystyle{ U' \subset \zeta(U_1')\! }[/math] such that [math]\displaystyle{ \zeta|_{\zeta^{-1}(U')}\! }[/math] is a diffeomorphism. Put [math]\displaystyle{ U = \phi_1^{-1}(\zeta^{-1}(U'))\! }[/math] and [math]\displaystyle{ \phi = \zeta \circ \phi_1|_U\! }[/math]. Then [math]\displaystyle{ \phi\! }[/math] is a chart.
It remains to check that [math]\displaystyle{ \pi \circ \phi = \psi \circ \theta|_U\! }[/math], but this is clear: if [math]\displaystyle{ (x,y) = \phi_1(q)\! }[/math] for some [math]\displaystyle{ q \in U\! }[/math], then [math]\displaystyle{ \pi\circ\phi(q) = \pi\circ\zeta(x,y) = \theta_1(x,y) = \psi(\theta(q))\! }[/math] by definition of [math]\displaystyle{ \theta_1\! }[/math]. [math]\displaystyle{ \Box\! }[/math]