0708-1300/Class notes for Tuesday, September 11

0708-1300/Navigation Panel   Add your name / see who's in! # Week of... Links Fall Semester 1 Sep 10 About, Tue, Thu 2 Sep 17 Tue, HW1, Thu 3 Sep 24 Tue, Photo, Thu 4 Oct 1 Questionnaire, Tue, HW2, Thu 5 Oct 8 Thanksgiving, Tue, Thu 6 Oct 15 Tue, HW3, Thu 7 Oct 22 Tue, Thu 8 Oct 29 Tue, HW4, Thu, Hilbert sphere 9 Nov 5 Tue,Thu, TE1 10 Nov 12 Tue, Thu 11 Nov 19 Tue, Thu, HW5 12 Nov 26 Tue, Thu 13 Dec 3 Tue, Thu, HW6 Spring Semester 14 Jan 7 Tue, Thu, HW7 15 Jan 14 Tue, Thu 16 Jan 21 Tue, Thu, HW8 17 Jan 28 Tue, Thu 18 Feb 4 Tue 19 Feb 11 TE2, Tue, HW9, Thu, Feb 17: last chance to drop class R Feb 18 Reading week 20 Feb 25 Tue, Thu, HW10 21 Mar 3 Tue, Thu 22 Mar 10 Tue, Thu, HW11 23 Mar 17 Tue, Thu 24 Mar 24 Tue, HW12, Thu 25 Mar 31 Referendum,Tue, Thu 26 Apr 7 Tue, Thu R Apr 14 Office hours R Apr 21 Office hours F Apr 28 Office hours, Final (Fri, May 2) Register of Good Deeds Errata to Bredon's Book

Announcements go here

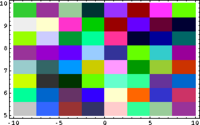
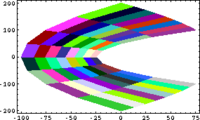
In Small Scales, Everything's Linear

	$\longrightarrow$
$z$	$\mapsto$	$z^{2}$

Code in Mathematica:

QuiltPlot[{f_,g_}, {x_, xmin_, xmax_, nx_}, {y_, ymin_, ymax_, ny_}] :=
Module[
  {dx, dy, grid, ix, iy},
  SeedRandom[1];
  dx=(xmax-xmin)/nx;
  dy=(ymax-ymin)/ny;
  grid = Table[
    {x -> xmin+ix*dx, y -> ymin+iy*dy},
    {ix, 0, nx}, {iy, 0, ny}
  ];
  grid = Map[({f, g} /. #)&, grid, {2}];
  Show[
    Graphics[Table[
      {
        RGBColor[Random[], Random[], Random[]],
        Polygon[{
          grid[[ix, iy]],
          grid[[ix+1, iy]],
          grid[[ix+1, iy+1]],
          grid[[ix, iy+1]]
        }]
      },
      {ix, nx}, {iy, ny}
    ]],
    Frame -> True
  ]
]

QuiltPlot[{x, y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
QuiltPlot[{x^2-y^2, 2*x*y}, {x, -10, 10, 8}, {y, 5, 10, 8}]

See also 06-240/Linear Algebra - Why We Care.

Class Notes

The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.

Differentiability

Let $U$, $V$ and $W$ be two normed finite dimensional vector spaces and let $f:V\rightarrow W$ be a function defined on a neighborhood of the point $x$.

Definition:

We say that $f$ is differentiable (diffable) at $x$ if there is a linear map $L$ so that

$\lim _{h\rightarrow 0}{\frac {|f(x+h)-f(x)-L(h)|}{|h|}}=0.$

In this case we will say that $L$ is a differential of $f$ at $x$ and will denote it by $df_{x}$.

Theorem

If $f:V\rightarrow W$ and $g:U\rightarrow V$ are diffable maps then the following asertions holds:

1. $df_{x}$ is unique.
2. $d(f+g)_{x}=df_{x}+dg_{x}$
3. If $f$ is linear then $df_{x}=f$
4. $d(f\circ g)_{x}=df_{g(x)}\circ dg_{x}$
5. For every scalar number $\alpha$ it holds $d(\alpha f)_{x}=\alpha df_{x}$

Implicit Function Theorem

Example Although $x^{2}+y^{2}=1$ does not defines $y$ as a function of $x$, in a neighborhood of $(0;-1)$ we can define $g(x)=-{\sqrt {1-x^{2}}}$ so that $x^{2}+g(x)^{2}=1$. Furthermore, $g$ is differentiable with differential $dg_{x}={\frac {x}{\sqrt {1-x^{2}}}}$. This is a motivation for the following theorem.

Notation

If $f:X\times Y\rightarrow Z$ then given $x\in X$ we will define $f_{[x]}:Y\rightarrow Z$ by $f_{[x]}(y)=f(x;y).$

Definition

$C^{p}(V)$ will be the class of all functions defined on $V$ with continuous partial derivatives up to order $p.$

Theorem(Implicit function theorem)

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f:\mathbb{R}^n \times \mathbb{R}^m\rightarrow \mathbb{R}^m} be a $C^{1}(\mathbb {R} ^{n}\times \mathbb {R} ^{m})$ function defined on a neighborhood $U$ of the point $(x_{0};y_{0})$ and such that $f(x_{0};y_{0})=0$ and suppose that $d(f_{[x]})_{y}$ is non-singular then, the following results holds:

There is an open neighborhood of $x_{0}$, $V\subset U$, and a diffable function $g:V\rightarrow \mathbb {R} ^{m}$ such that $g(x_{0})=y_{0}$ and for every $x\in V$ $f(x;g(x))=0.$.