0708-1300/Homework Assignment 6
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reading
At your leisure, read your class notes over the break, and especially at some point right before classes resume next semester. Here are a few questions you can ask yourself while reading:
- Do you understand pullbacks of differential forms?
- Do you think you could in practice integrate any differential form on any manifold (at least when the formulas involved are not too messy)?
- Do you understand orientations and boundaries and how they interact?
- Why is Stokes' theorem true? Both in terms of the local meaning of [math]\displaystyle{ d }[/math], and in terms of a formal proof.
- Do you understand the two and three dimensional cases of Stokes' theorem?
- Do you understand the Hodge star operator [math]\displaystyle{ \star }[/math]?
- How did we get [math]\displaystyle{ d\star dA=J }[/math] from the least action principle?
- Do you understand how Poincare's lemma entered the derivation of Maxewell's equations?
- Do you understand the operator [math]\displaystyle{ P }[/math]? (How was it used, formally derived, and what is the intuitive picture behind it?)
- What was [math]\displaystyle{ H_{dR} }[/math] and how did it relate to pullbacks and homotopy.
Doing
Solve the following problems and submit your solutions of problems 1, 3 and 4. This is a very challenging collection of problems; I expect most of you to do problem 2 with no difficulty (it is a repeat of an older problem), problem 1 with some effort, and I hope each of you will be able to do at least one further problem. It will be great if some of you will do all problems!
Problem 1. If [math]\displaystyle{ M }[/math] is a compact orientable [math]\displaystyle{ n }[/math]-manifold with no boundary, show that [math]\displaystyle{ H^n_{dR}(M)\neq 0 }[/math].
Problem 2. The standard volume form on [math]\displaystyle{ S^2 }[/math] is the form [math]\displaystyle{ \omega }[/math] given by [math]\displaystyle{ \omega=\frac{1}{4\pi}\left(xdy\wedge dz+ydz\wedge dx+zdx\wedge dy\right) }[/math]. Show that [math]\displaystyle{ \int_{S^2}\omega=1 }[/math].
Problem 3. Show that if [math]\displaystyle{ \omega\in\Omega^2(S^2) }[/math] satisfies [math]\displaystyle{ \int_{S_2}\omega=0 }[/math], then [math]\displaystyle{ \omega }[/math] is exact. Deduce that if [math]\displaystyle{ w_1\in\Omega^2(S^2) }[/math] and [math]\displaystyle{ w_2\in\Omega^2(S^2) }[/math] satisfy [math]\displaystyle{ \int_{S_2}\omega_1=\int_{S_2}\omega_2 }[/math], then [math]\displaystyle{ [\omega_1]=[\omega_2] }[/math] as elements of [math]\displaystyle{ H^2_{dR}(S^2) }[/math]. Deduce further that [math]\displaystyle{ \dim H^2_{dR}(S^2)=1 }[/math].
Problem 4. A "link" in [math]\displaystyle{ {\mathbb R}^3 }[/math] is an ordered pair [math]\displaystyle{ \gamma=(\gamma_1, \gamma_2) }[/math], in which [math]\displaystyle{ \gamma_1 }[/math] and [math]\displaystyle{ \gamma_2 }[/math] are smooth embeddings of the circle [math]\displaystyle{ S^1 }[/math] into [math]\displaystyle{ {\mathbb R}^3 }[/math], whose images (called "the components of [math]\displaystyle{ \gamma }[/math]") are disjoint. Two such links are called "isotopic", if one can be deformed to the other via a smooth homotopy along which the components remain embeddings and remain disjoint. Given a link [math]\displaystyle{ \gamma }[/math], define a map [math]\displaystyle{ \Phi_\gamma:S^1\times S^1\to S^2 }[/math] by [math]\displaystyle{ \Phi_\gamma(t_1,t_2):=\frac{\gamma_2(t_2)-\gamma_1(t_1)}{||\gamma_2(t_2)-\gamma_1(t_1)||} }[/math]. Finally, let [math]\displaystyle{ \omega }[/math] be the standard volume form of [math]\displaystyle{ S^2 }[/math], and define "the linking number of [math]\displaystyle{ \gamma=(\gamma_1, \gamma_2) }[/math]" to be [math]\displaystyle{ l(\gamma)=l(\gamma_1,\gamma_2):=\int_{S^1\times S^1}\Phi_\gamma^\star\omega }[/math]. Show
- If two links [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ \gamma' }[/math] are isotopic, then their linking numbers are the same: [math]\displaystyle{ l(\gamma)=l(\gamma') }[/math].
- If [math]\displaystyle{ \omega' }[/math] is a second 2-form on [math]\displaystyle{ S^2 }[/math] for which [math]\displaystyle{ \int_{S^2}\omega'=1 }[/math] and if [math]\displaystyle{ l'(\gamma) }[/math] is defined in the same manner as [math]\displaystyle{ l(\gamma) }[/math] except replacing [math]\displaystyle{ \omega }[/math] with [math]\displaystyle{ \omega' }[/math], then [math]\displaystyle{ l(\gamma)=l'(\gamma) }[/math]. (In particular this is true if [math]\displaystyle{ \omega' }[/math] is very close to a [math]\displaystyle{ \delta }[/math]-function form at the north pole of [math]\displaystyle{ S^2 }[/math]).
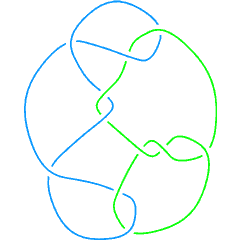
- Compute (but just up to an overall sign) the linking number of the link L11a193, displayed below:
|
|
|
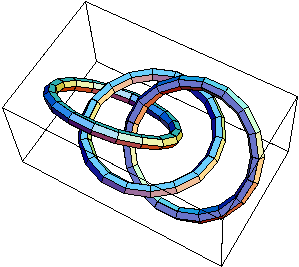
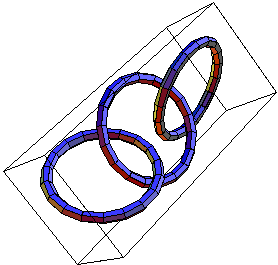
| The links L11a193, [math]\displaystyle{ \gamma_3 }[/math] and [math]\displaystyle{ \gamma'_3 }[/math]. | ||
Just for Fun
Prove that the two (3-component) links [math]\displaystyle{ \gamma_3 }[/math] and [math]\displaystyle{ \gamma'_3 }[/math] shown above are not isotopic, yet their complements are diffeomorphic. (See more at Classes: 2004-05: Math 1300Y - Topology: Homework Assignment 5)
Due Date
This assignment is due in class on Thursday January 10, 2007.
