0708-1300/Class notes for Thursday, October 4: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
==Movie Time== |
==Movie Time== |
||
With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's [http://www.geom.uiuc.edu/docs/outreach/oi/ home], a {{Home Link|Talks/UofT-040205/index.html|talk}} I once gave, and the [http://video.google.com/videoplay?docid=-6626464599825291409 movie] itself, on google video. |
With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's [http://www.geom.uiuc.edu/docs/outreach/oi/ home], a {{Home Link|Talks/UofT-040205/index.html|talk}} I once gave, and the [http://video.google.com/videoplay?docid=-6626464599825291409 movie] itself, on google video. |
||
==Class Notes== |
|||
===Definition=== |
|||
Let <math>\theta : M^m \rightarrow N^n\!</math> be a smooth map between manifolds. If for each <math>p \in M\!</math> the differential <math>d\theta_p : T_p M \rightarrow T_{\theta(p)} N\!</math> is surjective, <math>\theta\!</math> is called a <b>submersion</b>. |
|||
===Theorem=== |
|||
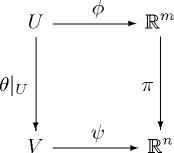
If <math>\theta : M^m \rightarrow N^n\!</math> is a smooth map between manifolds and for some <math>p \in M\!</math> the differential <math>d\theta_p : T_p M \rightarrow T_{\theta(p)} N\!</math> is surjective then there exist charts <math>\phi : U \rightarrow U' \subset \mathbb{R}^m\!</math> and <math>\psi : V \rightarrow V' \subset \mathbb{R}^n\!</math> on <math>M\!</math> and <math>N\!</math> respectively such that |
|||
<ol> |
|||
<li> <math>\phi(p) = 0\!</math> |
|||
<li> <math>\psi\left(\theta(p)\right) = 0\!</math> |
|||
<li> The diagram |
|||
<p align="center">[[Image:07-10-04-submersion-diagram.png]]</p> |
|||
<p> commutes, where <math>\pi : \mathbb{R}^m = \mathbb{R}^n \times \mathbb{R}^{m-n} \rightarrow \mathbb{R}^n\!</math> is the canonical projection. </p> |
|||
</ol> |
|||
====Proof==== |
|||
Revision as of 22:40, 4 October 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Movie Time
With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's home, a talk I once gave, and the movie itself, on google video.
Class Notes
Definition
Let be a smooth map between manifolds. If for each the differential is surjective, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} is called a submersion.
Theorem
If is a smooth map between manifolds and for some the differential is surjective then there exist charts and on and respectively such that
- The diagram
commutes, where is the canonical projection.
