0708-1300/Class notes for Tuesday, September 11: Difference between revisions
| Line 88: | Line 88: | ||
Let <math>f:\mathbb{R}^n \times \mathbb{R}^m\rightarrow \mathbb{R}^m</math> be a <math>C^{1}(\mathbb{R}^n \times \mathbb{R}^m)</math> function defined on a neighborhood <math>U</math> of the point <math>(x_0;y_0)</math> and such that <math>f(x_0;y_0)=0</math> and suppose that <math>d(f_{[x]})_{y}</math> is non-singular then, the following results holds: |
Let <math>f:\mathbb{R}^n \times \mathbb{R}^m\rightarrow \mathbb{R}^m</math> be a <math>C^{1}(\mathbb{R}^n \times \mathbb{R}^m)</math> function defined on a neighborhood <math>U</math> of the point <math>(x_0;y_0)</math> and such that <math>f(x_0;y_0)=0</math> and suppose that <math>d(f_{[x]})_{y}</math> is non-singular then, the following results holds: |
||
There is an open neighborhood of <math>x</math>, <math>V\subset U</math>, and a |
There is an open neighborhood of <math>x</math>, <math>V\subset U</math>, and a ''diffable'' function <math>g:V\rightarrow\mathbb{R}^m</math> such that for every <math>x\in V</math> <math>f(x;g(x))=0.</math>. |
||
Revision as of 21:51, 11 September 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
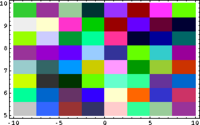
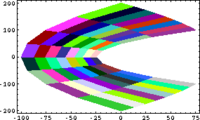
In Small Scales, Everything's Linear
|
| |
Code in Mathematica:
QuiltPlot[{f_,g_}, {x_, xmin_, xmax_, nx_}, {y_, ymin_, ymax_, ny_}] :=
Module[
{dx, dy, grid, ix, iy},
SeedRandom[1];
dx=(xmax-xmin)/nx;
dy=(ymax-ymin)/ny;
grid = Table[
{x -> xmin+ix*dx, y -> ymin+iy*dy},
{ix, 0, nx}, {iy, 0, ny}
];
grid = Map[({f, g} /. #)&, grid, {2}];
Show[
Graphics[Table[
{
RGBColor[Random[], Random[], Random[]],
Polygon[{
grid[[ix, iy]],
grid[[ix+1, iy]],
grid[[ix+1, iy+1]],
grid[[ix, iy+1]]
}]
},
{ix, nx}, {iy, ny}
]],
Frame -> True
]
]
QuiltPlot[{x, y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
QuiltPlot[{x^2-y^2, 2*x*y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
See also 06-240/Linear Algebra - Why We Care.
Class Notes
Differentiability
Let , and be two normed finite dimensional vector spaces and let be a function defined on a neighborhood of the point .
Definition:
We say that is differentiable (diffable) at if there is a linear map so that
In this case we will say that is a differential of at and will denote it by .
Theorem
If and are diffable maps then the following asertions holds:
- is unique.
- If is linear then
- For every scalar number it holds
Implicit Function Theorem
Example Although does not defines as a function of , in a neighborhood of we can define so that . Furthermore, is differentiable with differential . This is a motivation for the following theorem.
Notation
If f:X\times Y\rightarrow Z then given x\in X we will define f_{[x]}:Y\rightarrow Z by f_{[x]}(y)=f(x;y)
Definition
will be the class of all functions defined on with continuous partial derivatives up to order
Theorem(Implicit function theorem)
Let be a function defined on a neighborhood of the point and such that and suppose that is non-singular then, the following results holds:
There is an open neighborhood of , , and a diffable function such that for every .

































![{\displaystyle d(f_{[x]})_{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/286bcb64de94afff8f12a11dbb3341620bac0600)



