0708-1300/Homework Assignment 8: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
==Doing== |
==Doing== |
||
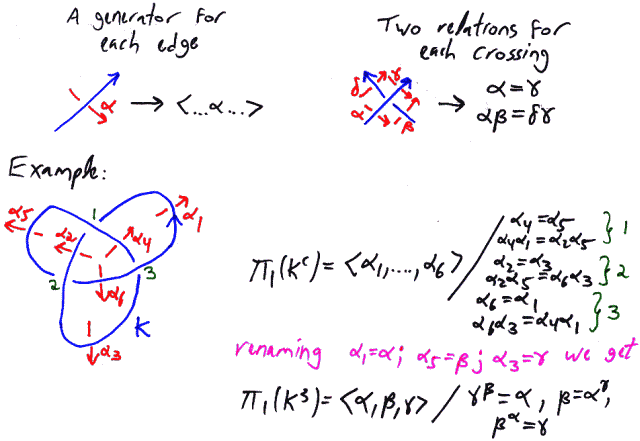
'''Just one problem.''' Let <math>K</math> be a knot in <math>{\mathbb R}^3</math> presented by a planar diagram <math>D</math>. With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of <math>K</math> has a presentation (the "Wirtinger" |
'''Just one problem.''' Let <math>K</math> be a knot in <math>{\mathbb R}^3</math> presented by a planar diagram <math>D</math>. With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of <math>K</math> has a presentation (the "Wirtinger" presentation) with one generator for each edge of <math>D</math> and two relations for each crossing of <math>D</math>, as indicated in the figure below. |
||
<center> |
<center> |
||
Revision as of 09:49, 24 January 2008
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The information below is preliminary and cannot be trusted! (v)
Reading
Read, reread and rereread your notes to this point, and make sure that you really, really really, really really really understand everything in them. Do the same every week!
Doing
Just one problem. Let [math]\displaystyle{ K }[/math] be a knot in [math]\displaystyle{ {\mathbb R}^3 }[/math] presented by a planar diagram [math]\displaystyle{ D }[/math]. With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of [math]\displaystyle{ K }[/math] has a presentation (the "Wirtinger" presentation) with one generator for each edge of [math]\displaystyle{ D }[/math] and two relations for each crossing of [math]\displaystyle{ D }[/math], as indicated in the figure below.
Due Date
This assignment is due in class on Thursday February 7, 2008.