0708-1300/Homework Assignment 6: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
'''Problem 1.''' If <math>M</math> is a compact orientable n-manifold with no boundary, show that <math>H^n_{dR}(M)\neq 0</math>. |
'''Problem 1.''' If <math>M</math> is a compact orientable n-manifold with no boundary, show that <math>H^n_{dR}(M)\neq 0</math>. |
||
'''Problem |
'''Problem 2.''' The "standard volume form on S^2" is the form <math>\omega</math> given by <math>\omega=\frac{1}{4\pi}\left(xdy\wedge dz+ydz\wedge dx+zdx\wedge dy\right)</math>. Show that <math>\int_{S^2}\omega=1</math>. |
||
'''Problem 3.''' Show that if <math>\omega\in\Omega^2(S^2)</math> satisfies <math>\int_{S_2}\omega=0</math>, then <math>\omega</math> is exact, and therefore, if <math>w_1\in\Omega^2(S^2)</math> and <math>w_2\in\Omega^2(S^2)</math> satisfy <math>\int_{S_2}\omega_1=\int_{S_2}\omega_2</math>, then <math>[\omega_1]=[\omega_2]</math> as elements of <math>H^n_{dR}(S^2)</math>. |
'''Problem 3.''' Show that if <math>\omega\in\Omega^2(S^2)</math> satisfies <math>\int_{S_2}\omega=0</math>, then <math>\omega</math> is exact, and therefore, if <math>w_1\in\Omega^2(S^2)</math> and <math>w_2\in\Omega^2(S^2)</math> satisfy <math>\int_{S_2}\omega_1=\int_{S_2}\omega_2</math>, then <math>[\omega_1]=[\omega_2]</math> as elements of <math>H^n_{dR}(S^2)</math>. |
||
Revision as of 18:24, 5 December 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The information below is preliminary and cannot be trusted! (v)
Reading
At your leisure, read your class notes over the break, and especially at some point right before classes resume after the break.
Doing
Solve and submit your solutions of the following problems:
Problem 1. If [math]\displaystyle{ M }[/math] is a compact orientable n-manifold with no boundary, show that [math]\displaystyle{ H^n_{dR}(M)\neq 0 }[/math].
Problem 2. The "standard volume form on S^2" is the form [math]\displaystyle{ \omega }[/math] given by [math]\displaystyle{ \omega=\frac{1}{4\pi}\left(xdy\wedge dz+ydz\wedge dx+zdx\wedge dy\right) }[/math]. Show that [math]\displaystyle{ \int_{S^2}\omega=1 }[/math].
Problem 3. Show that if [math]\displaystyle{ \omega\in\Omega^2(S^2) }[/math] satisfies [math]\displaystyle{ \int_{S_2}\omega=0 }[/math], then [math]\displaystyle{ \omega }[/math] is exact, and therefore, if [math]\displaystyle{ w_1\in\Omega^2(S^2) }[/math] and [math]\displaystyle{ w_2\in\Omega^2(S^2) }[/math] satisfy [math]\displaystyle{ \int_{S_2}\omega_1=\int_{S_2}\omega_2 }[/math], then [math]\displaystyle{ [\omega_1]=[\omega_2] }[/math] as elements of [math]\displaystyle{ H^n_{dR}(S^2) }[/math].
Problem 4. A "link" in [math]\displaystyle{ {\mathbb R}^3 }[/math] is an ordered pair [math]\displaystyle{ \gamma=(\gamma_1, \gamma_2) }[/math], in which [math]\displaystyle{ \gamma_1 }[/math] and [math]\displaystyle{ \gamma_2 }[/math] are smooth embeddings of the circle [math]\displaystyle{ S^1 }[/math] into [math]\displaystyle{ {\mathbb R}^3 }[/math], whose images (called "the components of [math]\displaystyle{ \gamma }[/math]") are disjoint. Two such links are called "isotopic", if one can be deformed to the other via a homotopy along which the components remain disjoint. Given a link [math]\displaystyle{ \gamma }[/math], define a map [math]\displaystyle{ \Phi_\gamma:S^1\times S^1\to S^2 }[/math] by [math]\displaystyle{ \Phi_\gamma(t_1,t_2):=\frac{\gamma_2(t_2)-\gamma_1(t_1)}{||\gamma_2(t_2)-\gamma_1(t_1)||} }[/math]. Finally, let [math]\displaystyle{ \omega }[/math] be the standard volume form of [math]\displaystyle{ S^2 }[/math], and define "the linking number of [math]\displaystyle{ \gamma=(\gamma_1, \gamma_2) }[/math]" to be [math]\displaystyle{ l(\gamma)=l(\gamma_1,\gamma_2):=\int_{S^1\times S^1}\Phi_\gamma^\star\omega }[/math]. Show
- If two links [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ \gamma' }[/math] are isotopic, then their linking numbers are the same: [math]\displaystyle{ l(\gamma)=l(\gamma') }[/math].
- If [math]\displaystyle{ \omega' }[/math] is a second 2-form on [math]\displaystyle{ S^2 }[/math] for which [math]\displaystyle{ \int_{S^2}\omega'=1 }[/math] and if [math]\displaystyle{ l'(\gamma) }[/math] is defined in the same manner as [math]\displaystyle{ l(\gamma) }[/math] except replacing [math]\displaystyle{ \omega }[/math] with [math]\displaystyle{ \omega' }[/math], then [math]\displaystyle{ l(\gamma)=l'(\gamma) }[/math]. (In particular this is true if [math]\displaystyle{ \omega' }[/math] is very close to a [math]\displaystyle{ \delta }[/math]-function form at the north pole of [math]\displaystyle{ S^2 }[/math]).
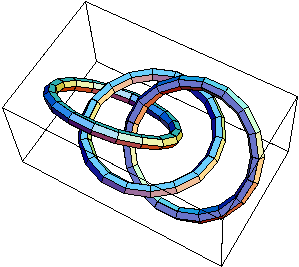
- Compute (but just up to an overall sign) the linking number of the link L11a193, displayed below:
Due Date
This assignment is due in class on Thursday January 10, 2007.
Just for Fun
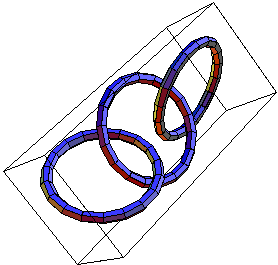
Prove that the following two links are not isotopic, yet their complements are diffeomorphic:
|
|
(See more at Classes: 2004-05: Math 1300Y - Topology: Homework Assignment 5)