0708-1300/Class notes for Thursday, September 20: Difference between revisions
No edit summary |
|||
| Line 9: | Line 9: | ||
==Exercise== |
==Exercise== |
||
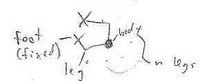
Configurations of a Generalized Cockroach (not entirely rigourous) |
|||
[[Image:0708-1300-Cockroach2.jpg|thumb|left|200px|Configurations of the Cockroach (page 2)]] |
|||
Let <math>C_n</math> be the manifold of configurations of a "cockroach" with <math>n</math> legs: |
|||
This is not entirely rigourous, and not a complete solution - it is (implicitly) assumed that the leg lengths and placement of the feet is "nice" in some ways, but with certain leg lengths and foot placements, you can either get a disconnected manifold or a single point. |
|||
[[Image:0708-1300-cockroach-labelling.jpg||center|200px|]] |
|||
Q: What is <math>C_n</math>? |
|||
In particular, what is <math>C_6</math>? |
|||
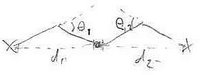
<math>n=2</math>: Consider <math>C_2</math>. |
|||
[[Image:0708-1300-cockroach-C2.jpg||left||200px]] |
|||
As in the picture, label the angles of the joints <math>\theta_1</math> and <math>\theta_2</math> and the distances from the body to the feet <math>d_1</math> and <math>d_2</math> respectively. |
|||
The value of <math>\theta_i</math> determines the value of <math>d_i</math>. |
|||
So, given values <math>(\theta_1, \theta_2)</math>, possible configurations are given by positions of the body, which must have distance <math>d_i</math> from the <math>i</math>th foot. |
|||
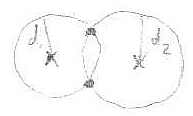
That is, the body must lie on the intersection of the two circles of radius <math>d_i</math> centred at the <math>i</math>th foot: |
|||
[[Image:0708-1300-cockroach-twocircles.jpg||center||]] |
|||
There are <math>0, 1, </math> or <math>2</math> solutions for the body position. |
|||
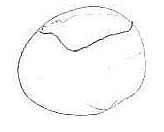
If we look only at the top body position, the pair <math>(\theta_1, \theta_2)</math> determines a unique configuration. |
|||
So, we can plot the subset on <math>\R^2_{(\theta_1,\theta_2)}</math>: |
|||
[[Image:0708-1300-cockroach-C2region.jpg||center||]] |
|||
The boundary points are where the "top" solution is in fact the unique solution. |
|||
By symmetry, taking the bottom solution gives us a similar region, and since the boundaries are where the top and bottom solutions coincide (there is only one solution along the boundary), the entire manifold is given by gluing the boundaries together. |
|||
This gives a sphere. |
|||
<math>n=3</math>: Configurations with <math>3</math> legs consist of a configuration with <math>2</math> legs plus the configuration of the third leg. |
|||
The configuration of the first <math>2</math> legs fixes the position of the body - and thus, the distance <math>d_3</math> from the third foot to the body. |
|||
For certain configurations of the first two legs, the body is too far from the third foot, so these are not found as part of configurations with three feet. |
|||
When the distance from the body to the third foot equals the length of the third leg completely extended, this gives a unique configuration of the <math>3</math>-legged cockroach. |
|||
Any closer and there are two possible configurations, corresponding to the two ways that the third joint can bend. |
|||
Let <math>R</math> be the region in <math>C_2 = S_2</math> where the distance to the third leg is close enough to give solutions. |
|||
The boundary of <math>R</math> is a curve, consisting of all the points at which there is a unique solution: |
|||
[[Image:0708-1300-cockroach-regionR.jpg||center||]] |
|||
So the manifold <math>C_3</math> is given by taking two copies of <math>R</math> and gluing their boundaries together. |
|||
This gives a sphere. |
|||
<math>n \geq 3</math>: Likewise, given that <math>C_n = S_2</math>, it follows that <math>C_{n+1} = S_2</math> also. |
|||
In particular, <math>C_6 = S_2</math>. |
|||
Revision as of 08:21, 23 September 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dror's Note
Come to my talk today at 4:30PM at the Fields Institute!
Class Notes
PDF file of the class notes typed up in latex can be located here
Tex version of the file is also avaliable here so that people can easily make changes and repost here if they wish.
Exercise
Configurations of a Generalized Cockroach (not entirely rigourous)
Let be the manifold of configurations of a "cockroach" with legs:
Q: What is ? In particular, what is ?
: Consider .
As in the picture, label the angles of the joints and and the distances from the body to the feet and respectively.
The value of determines the value of . So, given values , possible configurations are given by positions of the body, which must have distance from the th foot.
That is, the body must lie on the intersection of the two circles of radius centred at the th foot:
There are or solutions for the body position.
If we look only at the top body position, the pair determines a unique configuration.
So, we can plot the subset on :
The boundary points are where the "top" solution is in fact the unique solution.
By symmetry, taking the bottom solution gives us a similar region, and since the boundaries are where the top and bottom solutions coincide (there is only one solution along the boundary), the entire manifold is given by gluing the boundaries together. This gives a sphere.
: Configurations with legs consist of a configuration with legs plus the configuration of the third leg. The configuration of the first legs fixes the position of the body - and thus, the distance from the third foot to the body.
For certain configurations of the first two legs, the body is too far from the third foot, so these are not found as part of configurations with three feet. When the distance from the body to the third foot equals the length of the third leg completely extended, this gives a unique configuration of the -legged cockroach. Any closer and there are two possible configurations, corresponding to the two ways that the third joint can bend.
Let be the region in where the distance to the third leg is close enough to give solutions. The boundary of is a curve, consisting of all the points at which there is a unique solution:
So the manifold is given by taking two copies of and gluing their boundaries together. This gives a sphere.
: Likewise, given that , it follows that also. In particular, .