0708-1300/Class notes for Tuesday, September 11: Difference between revisions
| Line 50: | Line 50: | ||
==Class Notes== |
==Class Notes== |
||
=Differentiability= |
===Differentiability=== |
||
Let <math>U</math>, <math>V</math> and <math>W</math> be two normed finite dimensional vector spaces and let <math>f:V\rightarrow W</math> be a function defined on a neighborhood of the point <math>x</math> |
Let <math>U</math>, <math>V</math> and <math>W</math> be two normed finite dimensional vector spaces and let <math>f:V\rightarrow W</math> be a function defined on a neighborhood of the point <math>x</math> |
||
Revision as of 15:43, 11 September 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In Small Scales, Everything's Linear
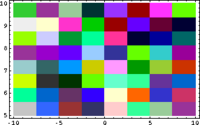
|
[math]\displaystyle{ \longrightarrow }[/math] | 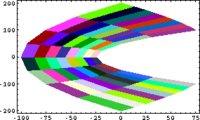
|
| [math]\displaystyle{ z }[/math] | [math]\displaystyle{ \mapsto }[/math] | [math]\displaystyle{ z^2 }[/math] |
Code in Mathematica:
QuiltPlot[{f_,g_}, {x_, xmin_, xmax_, nx_}, {y_, ymin_, ymax_, ny_}] :=
Module[
{dx, dy, grid, ix, iy},
SeedRandom[1];
dx=(xmax-xmin)/nx;
dy=(ymax-ymin)/ny;
grid = Table[
{x -> xmin+ix*dx, y -> ymin+iy*dy},
{ix, 0, nx}, {iy, 0, ny}
];
grid = Map[({f, g} /. #)&, grid, {2}];
Show[
Graphics[Table[
{
RGBColor[Random[], Random[], Random[]],
Polygon[{
grid[[ix, iy]],
grid[[ix+1, iy]],
grid[[ix+1, iy+1]],
grid[[ix, iy+1]]
}]
},
{ix, nx}, {iy, ny}
]],
Frame -> True
]
]
QuiltPlot[{x, y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
QuiltPlot[{x^2-y^2, 2*x*y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
See also 06-240/Linear Algebra - Why We Care.
Class Notes
Differentiability
Let [math]\displaystyle{ U }[/math], [math]\displaystyle{ V }[/math] and [math]\displaystyle{ W }[/math] be two normed finite dimensional vector spaces and let [math]\displaystyle{ f:V\rightarrow W }[/math] be a function defined on a neighborhood of the point [math]\displaystyle{ x }[/math]
Definition:
We say that [math]\displaystyle{ f }[/math] is differentiable (diffable) if there is a linear map [math]\displaystyle{ L }[/math] so that
[math]\displaystyle{ \lim_{h\rightarrow0}\frac{|f(x+h)-f(x)-L(h)|}{|h|}. }[/math]
In this case we will say that [math]\displaystyle{ L }[/math] is a differential of [math]\displaystyle{ f }[/math] and will denote it by [math]\displaystyle{ df_{x} }[/math].
Theorem
If [math]\displaystyle{ f:V\rightarrow W }[/math] and [math]\displaystyle{ g:U\rightarrow V }[/math] are diffable maps then the following asertions holds:
1)[math]\displaystyle{ df_{x} }[/math] is unique.
2)[math]\displaystyle{ d(f+g)_{x}=df_{x}+dg_{x} }[/math]
3)If [math]\displaystyle{ f }[/math] is linear then [math]\displaystyle{ df_{x}=f }[/math]
4)[math]\displaystyle{ d(f\circ g)_{x}=df_{g(x)}\circ dg_{x} }[/math]
5)For every scalar number [math]\displaystyle{ \alpha }[/math] it holds [math]\displaystyle{ d(\alpha f)_{x}=\alpha df_{x} }[/math]
