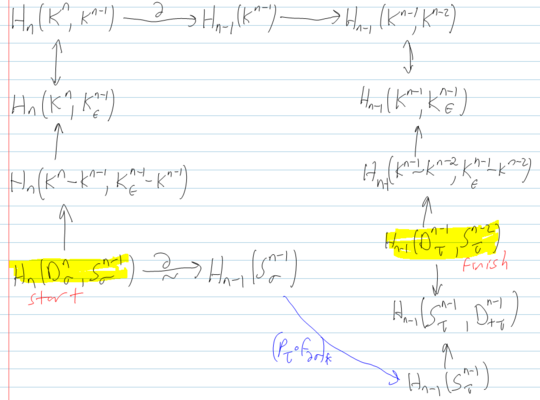0708-1300/Homework Assignment 12: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{0708-1300/Navigation}} |
{{0708-1300/Navigation}} |
||
{{In Preparation}} |
|||
==Reading== |
==Reading== |
||
Read, reread and rereread your notes to this point, and make sure that you really, really really, really really really understand everything in them. Do the same every week! |
Read, reread and rereread your notes to this point, and make sure that you really, really really, really really really understand everything in them. Do the same every week! Also, read section 8-11, 13 and 18-20 of chapter IV of Bredon's book (three times, as always). |
||
Also, read section 8-11, 13 and 18-20 of chapter IV of Bredon's book three times: |
|||
* First time as if you were reading a novel - quickly and without too much attention to detail, just to learn what the main keywords and concepts and goals are. |
|||
* Second time like you were studying for an exam on the subject - slowly and not skipping anything, verifying every little detail. |
|||
* And then a third time, again at a quicker pace, to remind yourself of the bigger picture all those little details are there to paint. |
|||
==Doing== |
==Doing== |
||
Solve all the problems in pages 206-207 of Bredon's book, but submit only your solutions of problems 1, 5, 9, and all the problems in pages 230 but submit only problem 1. |
Solve all the problems in pages 206-207 of Bredon's book, but submit only your solutions of problems 1, 5, 9, and all the problems in pages 230 but submit only problem 1. Also, solve and submit the following: |
||
Also, solve and submit the following: |
|||
'''Problem.''' Given a CW-space <math>K</math> with <math>n</math>-cells indexed by <math>K_n</math> and skeleta denoted <math>K^n</math>, show that the map <math>\partial_1:\langle K_n\rangle\to\langle K_{n-1}\rangle</math> given by the composition <math>H_n(K^n, K^{n-1})\longrightarrow H_{n-1}(K^{n-1})\longrightarrow H_{n-1}(K^{n-1}, K^{n-2})</math> is equal to the one defined using degrees: <math>\partial_2\sigma=\sum_{\tau\in K_{n-1}}[\tau:\sigma]\tau</math>, where <math>[\tau:\sigma]:=\deg p_\tau\circ f_{\partial\sigma}</math> and the <math>f_{\partial\sigma}</math>'s are the gluing maps defining <math>K</math>. |
'''Problem 12.''' Given a CW-space <math>K</math> with <math>n</math>-cells indexed by <math>K_n</math> and skeleta denoted <math>K^n</math>, show that the map <math>\partial_1:\langle K_n\rangle\to\langle K_{n-1}\rangle</math> given by the composition <math>H_n(K^n, K^{n-1})\longrightarrow H_{n-1}(K^{n-1})\longrightarrow H_{n-1}(K^{n-1}, K^{n-2})</math> is equal to the one defined using degrees: <math>\partial_2\sigma=\sum_{\tau\in K_{n-1}}[\tau:\sigma]\tau</math>, where <math>[\tau:\sigma]:=\deg p_\tau\circ f_{\partial\sigma}</math> and the <math>f_{\partial\sigma}</math>'s are the gluing maps defining <math>K</math>. |
||
'''Hint.''' {{Dror}}'s notes on the subject are: |
'''Hint.''' {{Dror}}'s notes on the subject are: |
||
[[Image:0708-1300-LongLoop.png|thumb|center| |
[[Image:0708-1300-LongLoop.png|thumb|center|540px|Divide and conquer!]] |
||
==Due Date== |
==Due Date== |
||
Latest revision as of 10:33, 27 March 2008
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reading
Read, reread and rereread your notes to this point, and make sure that you really, really really, really really really understand everything in them. Do the same every week! Also, read section 8-11, 13 and 18-20 of chapter IV of Bredon's book (three times, as always).
Doing
Solve all the problems in pages 206-207 of Bredon's book, but submit only your solutions of problems 1, 5, 9, and all the problems in pages 230 but submit only problem 1. Also, solve and submit the following:
Problem 12. Given a CW-space with -cells indexed by and skeleta denoted , show that the map given by the composition is equal to the one defined using degrees: , where and the 's are the gluing maps defining .
![{\displaystyle \partial _{2}\sigma =\sum _{\tau \in K_{n-1}}[\tau :\sigma ]\tau }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8418f07e3b03a3eae63fe0f70f5bd558b12bf2a0)
![{\displaystyle [\tau :\sigma ]:=\deg p_{\tau }\circ f_{\partial \sigma }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d834d77c4ac25d5346dc203cb0b1636dda637400)
Hint. Dror's notes on the subject are:
Due Date
This assignment is due in class on Thursday April 10, 2008.
