0708-1300/Homework Assignment 8: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{0708-1300/Navigation}} |
{{0708-1300/Navigation}} |
||
{{In Preparation}} |
|||
==Reading== |
==Reading== |
||
| Line 6: | Line 5: | ||
==Doing== |
==Doing== |
||
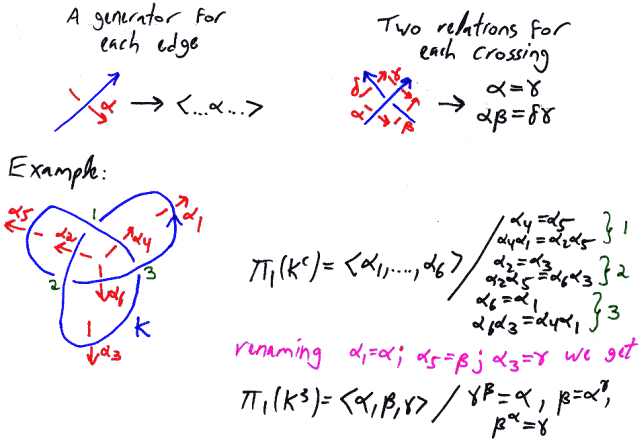
'''Just one problem.''' Let <math>K</math> be a knot in <math>{\mathbb R}^3</math> presented by a planar diagram <math>D</math>. With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of <math>K</math> has a presentation (the "Wirtinger" |
'''Just one problem.''' Let <math>K</math> be a knot in <math>{\mathbb R}^3</math> presented by a planar diagram <math>D</math>. With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of <math>K</math> has a presentation (the "Wirtinger" presentation) with one generator for each edge of <math>D</math> and two relations for each crossing of <math>D</math>, as indicated in the figure below. |
||
<center> |
<center> |
||
Latest revision as of 09:51, 24 January 2008
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reading
Read, reread and rereread your notes to this point, and make sure that you really, really really, really really really understand everything in them. Do the same every week!
Doing
Just one problem. Let be a knot in presented by a planar diagram . With a massive use of Van-Kampen's theorem, show that the fundamental group of the complement of has a presentation (the "Wirtinger" presentation) with one generator for each edge of and two relations for each crossing of , as indicated in the figure below.
Due Date
This assignment is due in class on Thursday February 7, 2008.