0708-1300/Homework Assignment 7: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{0708-1300/Navigation}} |
{{0708-1300/Navigation}} |
||
==Reading== |
|||
Quickly read section 1 of Chapter III of Bredon's book, and then |
|||
'''read''' sections 2-4 three times: |
|||
* First time as if you were reading a novel - quickly and without too much attention to detail, just to learn what the main keywords and concepts and goals are. |
|||
* Second time like you were studying for an exam on the subject - slowly and not skipping anything, verifying every little detail. |
|||
* And then a third time, again at a quicker pace, to remind yourself of the bigger picture all those little details are there to paint. |
|||
Also, '''pre-read''' (just once), the rest of chapter III. |
|||
==Doing== |
|||
Solve the following problems from Bredon's book, but submit only the solutions of the problems marked with an "S": |
|||
{|align=center border=1 cellspacing=0 cellpadding=5 |
|||
|- align=center |
|||
!Problems |
|||
!On page(s) |
|||
!Comments |
|||
|- align=center |
|||
|S1, S2, 3 |
|||
|138 |
|||
|"Topological groups" are defined in page 51. You need nothing beyond definition 15.1. |
|||
|- align=center |
|||
|1, S2, S3, 4 |
|||
|143 |
|||
| |
|||
|- align=center |
|||
|1, S2, 3 |
|||
|145-146 |
|||
| |
|||
|} |
|||
==Due Date== |
|||
This assignment is due in class on Thursday January 24, 2008. |
|||
==Just for fun== |
|||
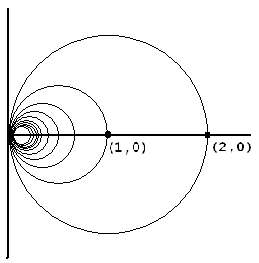
Prove that the fundamental group of the Hawaiian Earring, shown below, is uncountable. (The Hawaiian Earing is a countable union of circles shrinking to a point; the figure only shows the first few). |
|||
[[Image:0708-1300-HawaiianEarings.png|center]] |
|||
==Just to be Sure== |
==Just to be Sure== |
||
Visit [[0708-1300/Register of Good Deeds]] and complain if I didn't notice something. |
Visit [[0708-1300/Register of Good Deeds]] and complain if I didn't notice something. |
||
{{Dror/Students Divider}} |
|||
[[0708-1300/Hawaiian Earring|Here]] is an idea regarding the Hawaiian Earing but don't look at it until you think on the problem for a while. |
|||
Latest revision as of 21:49, 10 January 2008
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reading
Quickly read section 1 of Chapter III of Bredon's book, and then read sections 2-4 three times:
- First time as if you were reading a novel - quickly and without too much attention to detail, just to learn what the main keywords and concepts and goals are.
- Second time like you were studying for an exam on the subject - slowly and not skipping anything, verifying every little detail.
- And then a third time, again at a quicker pace, to remind yourself of the bigger picture all those little details are there to paint.
Also, pre-read (just once), the rest of chapter III.
Doing
Solve the following problems from Bredon's book, but submit only the solutions of the problems marked with an "S":
| Problems | On page(s) | Comments |
|---|---|---|
| S1, S2, 3 | 138 | "Topological groups" are defined in page 51. You need nothing beyond definition 15.1. |
| 1, S2, S3, 4 | 143 | |
| 1, S2, 3 | 145-146 |
Due Date
This assignment is due in class on Thursday January 24, 2008.
Just for fun
Prove that the fundamental group of the Hawaiian Earring, shown below, is uncountable. (The Hawaiian Earing is a countable union of circles shrinking to a point; the figure only shows the first few).
Just to be Sure
Visit 0708-1300/Register of Good Deeds and complain if I didn't notice something.
| Dror's notes above / Student's notes below |
Here is an idea regarding the Hawaiian Earing but don't look at it until you think on the problem for a while.