0708-1300/Class notes for Thursday, October 4: Difference between revisions
No edit summary |
m (→Theorem) |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
==Movie Time== |
==Movie Time== |
||
With the word "immersion" in our minds, we watch the movie "Outside In". Also see [http://www.geom.uiuc.edu/docs/outreach/oi/], |
With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's [http://www.geom.uiuc.edu/docs/outreach/oi/ home], a {{Home Link|Talks/UofT-040205/index.html|talk}} I once gave, and the [http://video.google.com/videoplay?docid=-6626464599825291409 movie] itself, on google video. |
||
==Class Notes== |
|||
<span style="color: red;">The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.</span> |
|||
<p>During the previous class, we discussed immersions---smooth maps whose differentials are injective. This class deals with the dual notion of submersions, defined as follows:</p> |
|||
===Definition=== |
|||
<p>Let <math>\theta : M^m \rightarrow N^n\!</math> be a smooth map between manifolds. If for each <math>p \in M\!</math> the differential <math>d\theta_p : T_p M \rightarrow T_{\theta(p)} N\!</math> is surjective, <math>\theta\!</math> is called a <b>submersion</b>. </p> |
|||
===Remarks=== |
|||
<p>We had previously seen that immersions induce "nice" coordinate charts---ones where the immersion looks like the canonical inclusion <math>\iota:\mathbb{R}^m\rightarrow\mathbb{R}^n</math> (where <math>n \ge m\!</math>). The proof of this theorem made use of the Inverse Function Theorem on a function defined on a chart of <math>N\!</math>. In the case of submersions, there is a similar theorem. Submersions locally look like the canonical projection <math>\pi : \mathbb{R}^m = \mathbb{R}^n \times \mathbb{R}^{m-n} \rightarrow \mathbb{R}^n\!</math>, and the proof of this fact makes use of the Inverse Function Theorem for a function define on a chart of <math>M\!</math> (duality!). However, before we can prove this theorem, we will need the following lemma.</p> |
|||
===Lemma=== |
|||
<p> Let <math>V\!</math> and <math>W\!</math> be finite-dimensional vector spaces over <math>\mathbb{R}\!</math> and let <math>T:V \rightarrow W \!</math> be a surjective linear map. Then there exist bases <math>v=\{v_1,\ldots,v_m\}\!</math> for <math>V\!</math> and <math>w=\{w_1,\ldots,w_n\}\!</math> for <math>W\!</math> such that the matrix representative of <math>T\!</math> with respect to <math>v\!</math> and <math>w\!</math> is that of the canonical projection <math>\pi : \mathbb{R}^m \rightarrow \mathbb{R}^n\!</math>.</p> |
|||
====Proof==== |
|||
<p>Let <math>w=\{w_1,\ldots,w_n\}\!</math> be any basis for <math>W\!</math> and choose <math>\{v_1,\ldots,v_n\} \subset V\!</math> such that <math>T(v_i)=w_i\!</math> for each <math>i\in\{1,\ldots,n\}\!</math> (this may be done since <math>T\!</math> is surjective). We claim that the set <math>v' = \{v_1,\ldots,v_n\} \subset V\!</math> is linearly independent. Suppose it were not. Then there would exist <math>\{c_1,\ldots,c_n\} \subset \mathbb{R}\!</math> with <math>\sum_{i=1}^n c_i v_i = 0\!</math> and <math>c_i \ne 0\!</math> for some <math>i\in\{1,\ldots,n\}\!</math>. But then <math>0 = T\left(\sum_{i=1}^n c_i v_i\right) = \sum_{i=1}^n c_i T\left( v_i\right) = \sum_{i=1}^n c_i w_i\!</math> by linearity of <math>T\!</math>, contradicting the assumption that <math>w\!</math> is a basis.</p> |
|||
<br> |
|||
<p> Note that <math>\mathrm{dim}(\mathrm{ker}(T)) = m-n\!</math>. Hence we may find a basis <math>v'' = \{v_{n+1},\ldots,v_m\} \subset V\!</math> for <math>\mathrm{ker}(T)\!</math>. Since <math>\mathrm{span}(v') \cap \mathrm{ker}(T) = \{0 \in V\}\!</math>, the set <math>v = v' \cup v''</math> must be linearly independent and hence form a basis for <math>V\!</math>. We then have <math>w_i = \sum_{i=j}^m \delta_{ij} T(v_j)\!</math>, so that the matrix representative of <math>T\!</math> is <math>\left( I_{n \times n} | 0_{n \times (m-n)} \right)\!</math>, which is the matrix representative of <math>\pi\!</math>. <math>\Box\!</math></p> |
|||
===Theorem=== |
|||
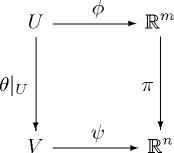
<p>If <math>\theta : M^m \rightarrow N^n\!</math> is a smooth map between manifolds and for some <math>p \in M\!</math> the differential <math>d\theta_p : T_p M \rightarrow T_{\theta(p)} N\!</math> is surjective then there exist charts <math>\phi : U \rightarrow U' \subset \mathbb{R}^m\!</math> and <math>\psi : V \rightarrow V' \subset \mathbb{R}^n\!</math> on <math>M\!</math> and <math>N\!</math>, respectively, such that</p> |
|||
<ol> |
|||
<li> <math>\phi(p) = 0\!</math> |
|||
<li> <math>\psi\left(\theta(p)\right) = 0\!</math> |
|||
<li> The diagram |
|||
<p align="center">[[Image:07-10-04-submersion-diagram.png]]</p> |
|||
<p> commutes, where <math>\pi : \mathbb{R}^m = \mathbb{R}^n \times \mathbb{R}^{m-n} \rightarrow \mathbb{R}^n\!</math> is the canonical projection. </p> |
|||
</ol> |
|||
====Proof==== |
|||
<p>Since translations are diffeomorphisms of <math>\mathbb{R}^k\!</math> for every <math>k \in \mathbb{N}\!</math>, it is trivial to find charts <math>\phi_0 : U_0 \rightarrow U_0' \subset \mathbb{R}^m\!</math> and <math>\psi : V \rightarrow V' \subset \mathbb{R}^m\!</math> such that <math>\phi(p) = 0 \in \mathbb{R}^m\!</math> and <math>\psi(\theta(p)) = 0 \in \mathbb{R}^n\!</math>. Furthermore, <math>V\!</math> is open, <math>U_0\!</math> is open and <math>\theta\!</math> is continuous, so <math>U_0 \cap \theta^{-1}\left(V\right) \subset M\!</math> is open and contains <math>p\!</math>. Hence, we may assume <math>U_0 \subset \theta^{-1}\left(V\right)\!</math> without loss of generality.</p> |
|||
<br> |
|||
<p>Let <math>\theta_0 = \psi \circ \theta \circ \phi_0^{-1} : U_0' \rightarrow V'\!</math> be the local representative of <math>\theta\!</math> and let <math>D_0 : \mathbb{R}^m \rightarrow \mathbb{R}^n \!</math> be the local representative of <math>d\theta_p\!</math>. Since <math>d\theta_p\!</math> is onto, we may apply the previous lemma to obtain a change of coordinates <math>T : \mathbb{R}^m \rightarrow \mathbb{R}^m</math> such that <math>D_0 = \pi \circ T</math>. </p> |
|||
<br> |
|||
<p>Let <math>\phi_1 = T \circ \phi_0\! : U_0 \rightarrow U_1' \subset \mathbb{R}^m</math>. Then <math>\phi_1\!</math> is a chart because <math>T\!</math> is a diffeomorphism. Let <math>\theta_1 = \psi \circ \theta \circ \phi_1^{-1} : U_1' \rightarrow V'\!</math> be the corresponding local representative, define <math>\zeta : U_1' \rightarrow \mathbb{R}^m\!</math> by <math>\zeta(x,y) = (\theta_1(x,y),y)\!</math>, and let <math>D_1 : \mathbb{R}^m \rightarrow \mathbb{R}^n\!</math> be the differential of <math>\theta_1\!</math> at <math>0\!</math>. Then, by construction of <math>T\!</math>, we have that <math>D_1 = \pi\!</math> and hence <math>d \zeta_0 = \mathrm{id}_{\mathbb{R}^m}\!</math>, which is invertible. Hence, the Inverse Function Theorem gives the existence of non-empty open set <math>U' \subset \zeta(U_1')\!</math> such that <math>\zeta|_{\zeta^{-1}(U')}\!</math> is a diffeomorphism. Put <math>U = \phi_1^{-1}(\zeta^{-1}(U'))\!</math> and <math>\phi = \zeta \circ \phi_1|_U\!</math>. Then <math>\phi\!</math> is a chart.</p> |
|||
<br> |
|||
<p>It remains to check that <math>\pi \circ \phi = \psi \circ \theta|_U\!</math>, but this is clear: if <math>\phi_1(q)=(x,y)\!</math> for some <math>q \in U\!</math>, then <math>\pi\circ\phi(q) = \pi\circ\zeta(x,y) = \theta_1(x,y) = \psi(\theta(q))\!</math> by definition of <math>\theta_1\!</math>. Hence, <math>\pi \circ \phi = \psi \circ \theta|_U\!</math> and the proof is complete.<math>\Box\!</math> |
|||
Latest revision as of 12:58, 8 October 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Movie Time
With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's home, a talk I once gave, and the movie itself, on google video.
Class Notes
The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.
During the previous class, we discussed immersions---smooth maps whose differentials are injective. This class deals with the dual notion of submersions, defined as follows:
Definition
Let be a smooth map between manifolds. If for each the differential is surjective, is called a submersion.
Remarks
We had previously seen that immersions induce "nice" coordinate charts---ones where the immersion looks like the canonical inclusion (where ). The proof of this theorem made use of the Inverse Function Theorem on a function defined on a chart of . In the case of submersions, there is a similar theorem. Submersions locally look like the canonical projection , and the proof of this fact makes use of the Inverse Function Theorem for a function define on a chart of (duality!). However, before we can prove this theorem, we will need the following lemma.
Lemma
Let and be finite-dimensional vector spaces over and let be a surjective linear map. Then there exist bases for and for such that the matrix representative of with respect to and is that of the canonical projection .
Proof
Let be any basis for and choose such that for each (this may be done since is surjective). We claim that the set is linearly independent. Suppose it were not. Then there would exist with and for some . But then by linearity of , contradicting the assumption that is a basis.
Note that . Hence we may find a basis for . Since , the set must be linearly independent and hence form a basis for . We then have , so that the matrix representative of is , which is the matrix representative of .
Theorem
If is a smooth map between manifolds and for some the differential is surjective then there exist charts and on and , respectively, such that
- The diagram
commutes, where is the canonical projection.
Proof
Since translations are diffeomorphisms of for every , it is trivial to find charts and such that and . Furthermore, is open, is open and is continuous, so is open and contains . Hence, we may assume without loss of generality.
Let be the local representative of and let be the local representative of . Since is onto, we may apply the previous lemma to obtain a change of coordinates such that .
Let . Then is a chart because is a diffeomorphism. Let be the corresponding local representative, define by , and let be the differential of at . Then, by construction of , we have that and hence , which is invertible. Hence, the Inverse Function Theorem gives the existence of non-empty open set such that is a diffeomorphism. Put and . Then is a chart.
It remains to check that , but this is clear: if for some , then by definition of . Hence, and the proof is complete.
