0708-1300/Class notes for Tuesday, January 22

0708-1300/Navigation Panel   Add your name / see who's in! # Week of... Links Fall Semester 1 Sep 10 About, Tue, Thu 2 Sep 17 Tue, HW1, Thu 3 Sep 24 Tue, Photo, Thu 4 Oct 1 Questionnaire, Tue, HW2, Thu 5 Oct 8 Thanksgiving, Tue, Thu 6 Oct 15 Tue, HW3, Thu 7 Oct 22 Tue, Thu 8 Oct 29 Tue, HW4, Thu, Hilbert sphere 9 Nov 5 Tue,Thu, TE1 10 Nov 12 Tue, Thu 11 Nov 19 Tue, Thu, HW5 12 Nov 26 Tue, Thu 13 Dec 3 Tue, Thu, HW6 Spring Semester 14 Jan 7 Tue, Thu, HW7 15 Jan 14 Tue, Thu 16 Jan 21 Tue, Thu, HW8 17 Jan 28 Tue, Thu 18 Feb 4 Tue 19 Feb 11 TE2, Tue, HW9, Thu, Feb 17: last chance to drop class R Feb 18 Reading week 20 Feb 25 Tue, Thu, HW10 21 Mar 3 Tue, Thu 22 Mar 10 Tue, Thu, HW11 23 Mar 17 Tue, Thu 24 Mar 24 Tue, HW12, Thu 25 Mar 31 Referendum,Tue, Thu 26 Apr 7 Tue, Thu R Apr 14 Office hours R Apr 21 Office hours F Apr 28 Office hours, Final (Fri, May 2) Register of Good Deeds Errata to Bredon's Book

Announcements go here

Pictures for a Van-Kampen Computation

In[1]:=

<< KnotTheory`

Loading KnotTheory` version of January 13, 2008, 20:30:12.1353.
Read more at http://katlas.org/wiki/KnotTheory.

In[2]:=	TubePlot[TorusKnot[8, 3]]
Out[2]=

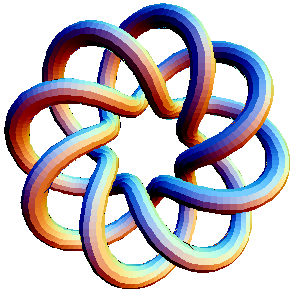
In[3]:=

TC[r1_, t1_,r2_,t2_ ] := { (r1 +r2 Cos[2Pi t2])Cos[2Pi t1], (r1 +r2 Cos[2Pi t2])Sin[2Pi t1], r2 Sin[2Pi t2] };

In[4]:=

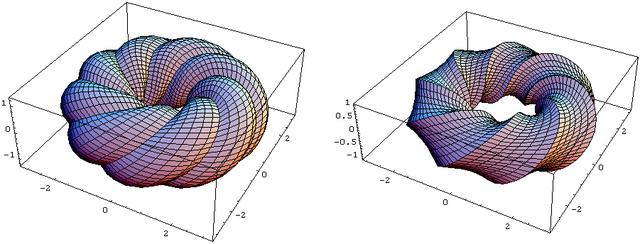
InflatedTorus[p_, q_, b_] := ParametricPlot3D[ TC[ 2, p t - q s, 1 + b(p^2 + q^2)s(1 - (p^2 + q^2)s), q t + p s ], {t, 0, 1}, {s, 0, 1/(p^2 + q^2)}, PlotPoints -> {6(p^2 + q^2) + 1, 7}, DisplayFunction -> Identity ];

In[5]:=	GraphicsArray[{{InflatedTorus[3,8,1], InflatedTorus[3,8,-1]}}]
Out[5]=

Typed Notes

First Hour

Today's Agenda:

1) More Examples of Van-Kampen Theorem

2) More Diagrams

3) Proof of Van-Kampen (was not done)

We began by recalling the examples from last class. I will not repeat that here, merely making a few additional comments that came out:

Notation:

Technically, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A*_H B} is poor notion as it implies that knowledge of A, B and H is sufficient to construct Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A*_H B} . In fact, we ALSO need to know the maps from H into A and B respectively in order for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A*_H B} to be defined.

Aside

Last class we simply wrote down the schematic for the two holed torus as an octagon with the identifications on the edges given last class. We now consider how one arrives at this schematic.

To create the two holed torus one begins with two tori. One then cuts out a small open disk from each torus and then glues the two boundaries together. Let us consider what this looks like when considering a torus as the normal schematic with a square in the plane with the normal identification of the sides. Removing an open disk is equivalent to removing the inside of a loop starting at one of the corners and finishing at that same corner. This is equivalent to making a pentagon with sides Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle aba^{-1}b^{-1}c} where c is the added edge.

Consider two such pentagons, gluing along the edge c forms precisely the octagon we had for the two holed torus last class.

Proposition

Letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma_g} denote the g holed torus, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma_g\neq\Sigma_{g'}}

(Note, I used the symbol $\neq$ to as the normal \ncong command doesn't seem to work. Take its meaning in context.)

Aside: Consider a functor from the category of groups to the category of Abelian groups via

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G\mapsto G^{ab} = G/(ab=ba)}

If we have a (homo)morphism from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G\rightarrow H} then the functor takes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\rightarrow H^{ab}} and yields a map Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{ab}\rightarrow H^{ab}} such that everything commutes.

Hence we know that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1^{ab}(\Sigma_g) \cong \mathbb{Z}^{2g}\neq\mathbb{Z}^{2g'} \cong\pi_1^{ab}(\Sigma_{g'})}

Of course, we need to know that in fact $\mathbb {Z} ^{m}\neq \mathbb {Z} ^{n}$ if $m\neq n$

As such, since the abelianizations are not isomorphic,neither are the original groups and the spaces themselves are not homeomorphic.

Example

$\pi _{1}(\mathbb {R} P^{2})$ is $\pi _{1}$ of the space which can be written as a disk with two antipodal points on the boundary circle on it with the identification that the top path a (going clockwise along the boundary) is glued to the bottom path (also going clock wise). But $\pi _{1}$ of this is just $<a>/(a^{2}=e)\cong \mathbb {Z} /2$

Claim:

Puncturing an n-manifold, $n\geq 3$, does not change $\pi _{1}(M)$. I.e., if $p\in M^{n}$ then $\pi _{1}(M)\cong \pi _{1}(M-\{p\})$

Proof:

Let $U_{1}=M-\{p\}$

$U_{2}$ = a coordinate patch about p.

Then $U_{1}\cap U_{2}=B^{n}-\{p\}\cong S^{n-1}$

If n=3, $\pi _{1}(S^{2})=\{e\}$ as we have computed before.

Hence, $\pi _{1}(M)=\pi _{1}(U_{1})*_{\{\}}\{\}=\pi _{1}(U_{1})$

Now, $\pi _{1}(S^{3})\cong \pi _{1}(S^{3}-\{p\})=\pi _{1}(B^{3})=\{e\}$

Continuing inductively the theorem holds for all n.

Aside:

If X is connected and $b_{1},\ b_{2}\in X$ then $\pi _{1}(X,b_{1})=\pi _{1}(X,b_{2})$. I.e., it does not matter which base point we choose in a connected space, the fundamental group is invariant of this.

Proof

Consider a path $\eta$ from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2} . The returning path is denoted Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{\eta}}

Consider a loop from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2} called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} .

Then get a loop from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1} via Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma\mapsto \bar{\eta}\gamma\eta}

Similarly about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2, \gamma\mapsto\eta\gamma\bar{\eta}}

Considering the composition we get $\eta {\bar {\eta }}\gamma \eta {\bar {\eta }}\sim \gamma$.

Second Hour

Claim

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^3} is the union (with common boundary) of two solid tori Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^1\times D^1}

The natural way to add two tori with common boundary would be two glue the boundaries of two disks (making Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^2} ) together for each angle going around the torus thus yielding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^1\times S^2} . Clearly this is not the same as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^3} as the fundamental groups differ.

Instead consider the following description. Look at a torus in the zx plane, this looks like two disks with the z axis in between them such that rotating these two disks about the z axis will yield the torus.

Lets now add in the second torus into this picture. We first draw a horizontal line between the two disks. We then "blow" up from beneath so the horizontal line is slightly curved. We imagine continuing to blow yielding larger and larger loops between the two disks until it "pops" forming the pure horizontal line consisting of the loop at infinity. Do the same for the bottom. Hence, the boundaries of the two tori drawn this way clearly are the same, and between the two cover the entire zx plane (and "point at infinity). Rotating this picture about the z axis yields all of S^1 as the union of these two sets.

Claim:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(S^3) = \{e\}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_1} = the normal solid torus thickened a bit and under Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1} yields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\alpha>}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_2} = the other solid torus, also thickened a bit, under $\pi _{1}$ yields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\beta>} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_1\cap U_2} is a normal torus only with slightly thick walls opposed to infinitely thin ones (homotopically the same)

So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(U_1\cap U_2)\cong\mathbb{Z}^2 \cong <a,b>/ab=ba}

So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(S^3) \cong\mathbb{Z}*_{\mathbb{Z}\times\mathbb{Z}}\mathbb{Z}}

However, we still need to describe Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{1*}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{2*}}

Do do this let me describe a,b,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} explicitly.

Considering the description of the two tori given above, we let a go around the outside of one of the two disks in the plane and b go from a point on the boundary of the same disk, following the rotation about the z axis, to a point on the boundary of the other dis. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is similar to b, but thought of as being on the boundary of the OTHER torus. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} consists of the path along the z axis.

Hence,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{1*}:}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\rightarrow e}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\rightarrow \alpha}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{2*}:}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\rightarrow\beta}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\rightarrow e} (as it is contractible)

Hence, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(S^3) = F(\alpha, \beta)/(e=\beta, \alpha = e)}

Hence, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(S^3) = \{e\}}

Example

Define the "Torus knot Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}} " where p and q are relatively prime integers. The knot Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{8,3}} is given above. We can think of this in the following ways:

1) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}} is the knot that wraps around the torus p times one way and q times the other way.

2) Formally, let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma:S^1\times S^1\mathbb{R}^3} be standard embedding of a torus. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma:[0,1]\rightarrow S^1\times S^1} be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\rightarrow (e^{2\pi i pt}, e^{i2\pi qt})}

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\circ\gamma}

3) Recall that the torus can be thought of as the image of the mapping Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^2\rightarrow\mathbb{R}^2/\mathbb{Z}^2}

Consider the rectangle in the real plane: ([0,p],[0,q]) and consider the path which is the diagonal line from the corner (0,0) to the corner (p,q)

No two points on this line are the same under the mapping down to the torus. If they were, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta y} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} would be integers and hence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta y/\Delta x} would be the slope of the line. But the slope of the line is q/p which is already in lowest common terms by assumption.

Lets compute the fundamental group of the compliment of the torus knot.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(\mathbb{R}^3-T_{p,q})\cong\pi_1(S^3-T_{p,q})}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_1} : inflated bagel, constrained by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_2} : inflated bubble constrained by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}}

(See top of page for pictures)

The intersection Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_1\cap U_2} looks somewhat like a belt. It has some thickness to it and is wrapped around the torus, eventually forming a loop. Hence it looks like a squashed disk cross a circle. Hence, under Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1} this is just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{Z}\cong<\gamma>} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} is the path parallel to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}}

We thus get the maps,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{1*}: \gamma\mapsto\alpha^p}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{2*}:\gamma\mapsto\beta^q}

Hence, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi_1(T_{p,q}^c) = <\alpha,\beta>/\alpha^p = \beta^q}

Thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{p,q}\neq T_{p',q'}}

Diagrams:

Recall our diagram from last class:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} &\ \ \ \ U_1&&\\ &\nearrow^{i_1}&\searrow^{j_1}&\\ U_1\cap U_2&&&U_1\cup U_2\\ &\searrow_{i_2}&\nearrow^{j_2}&\\ &\ \ \ \ U_2&&\\ \end{matrix}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_1\cup U_2} can be defined as the object such that the above diagram commutes and should the following commute:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} &\ \ \ \ U_1&&\\ &\nearrow^{i_1}&\searrow^{j_1}&\\ U_1\cap U_2&&&Y\\ &\searrow_{i_2}&\nearrow^{j_2}&\\ &\ \ \ \ U_2&&\\ \end{matrix}}

Then there is a unique map between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_1\cup U_2} and Y such that the composed diagram commutes.

Indeed, the same is true for general categories.

For

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} &\ \ \ \ G_1&&\\ &\nearrow^{i_1}&\searrow^{j_1}&\\ H&&&P\\ &\searrow_{i_2}&\nearrow^{j_2}&\\ &\ \ \ \ G_2&&\\ \end{matrix}}

commuting, P is defined as an object such that if also

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} &\ \ \ \ G_1&&\\ &\nearrow^{i_1}&\searrow^{j_1}&\\ H&&&Q\\ &\searrow_{i_2}&\nearrow^{j_2}&\\ &\ \ \ \ G_2&&\\ \end{matrix}}

were to commute then there is a unique morphism from P to Q such that the composed diagram computes.

In the category of groups, this "pushforward" P is unique and is isomorphic to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_1*_H G_2}