0708-1300/Class notes for Thursday, October 4

0708-1300/Navigation Panel   Add your name / see who's in! # Week of... Links Fall Semester 1 Sep 10 About, Tue, Thu 2 Sep 17 Tue, HW1, Thu 3 Sep 24 Tue, Photo, Thu 4 Oct 1 Questionnaire, Tue, HW2, Thu 5 Oct 8 Thanksgiving, Tue, Thu 6 Oct 15 Tue, HW3, Thu 7 Oct 22 Tue, Thu 8 Oct 29 Tue, HW4, Thu, Hilbert sphere 9 Nov 5 Tue,Thu, TE1 10 Nov 12 Tue, Thu 11 Nov 19 Tue, Thu, HW5 12 Nov 26 Tue, Thu 13 Dec 3 Tue, Thu, HW6 Spring Semester 14 Jan 7 Tue, Thu, HW7 15 Jan 14 Tue, Thu 16 Jan 21 Tue, Thu, HW8 17 Jan 28 Tue, Thu 18 Feb 4 Tue 19 Feb 11 TE2, Tue, HW9, Thu, Feb 17: last chance to drop class R Feb 18 Reading week 20 Feb 25 Tue, Thu, HW10 21 Mar 3 Tue, Thu 22 Mar 10 Tue, Thu, HW11 23 Mar 17 Tue, Thu 24 Mar 24 Tue, HW12, Thu 25 Mar 31 Referendum,Tue, Thu 26 Apr 7 Tue, Thu R Apr 14 Office hours R Apr 21 Office hours F Apr 28 Office hours, Final (Fri, May 2) Register of Good Deeds Errata to Bredon's Book

Announcements go here

Movie Time

With the word "immersion" in our minds, we watch the movie "Outside In". Also see the movie's home, a talk I once gave, and the movie itself, on google video.

Class Notes

The notes below are by the students and for the students. Hopefully they are useful, but they come with no guarantee of any kind.

Definition

Let [math]\displaystyle{ \theta : M^m \rightarrow N^n\! }[/math] be a smooth map between manifolds. If for each [math]\displaystyle{ p \in M\! }[/math] the differential [math]\displaystyle{ d\theta_p : T_p M \rightarrow T_{\theta(p)} N\! }[/math] is surjective, [math]\displaystyle{ \theta\! }[/math] is called a submersion.

Theorem

If [math]\displaystyle{ \theta : M^m \rightarrow N^n\! }[/math] is a smooth map between manifolds and for some [math]\displaystyle{ p \in M\! }[/math] the differential [math]\displaystyle{ d\theta_p : T_p M \rightarrow T_{\theta(p)} N\! }[/math] is surjective then there exist charts [math]\displaystyle{ \phi : U \rightarrow U' \subset \mathbb{R}^m\! }[/math] and [math]\displaystyle{ \psi : V \rightarrow V' \subset \mathbb{R}^n\! }[/math] on [math]\displaystyle{ M\! }[/math] and [math]\displaystyle{ N\! }[/math] respectively such that

1. [math]\displaystyle{ \phi(p) = 0\! }[/math]
2. [math]\displaystyle{ \psi\left(\theta(p)\right) = 0\! }[/math]
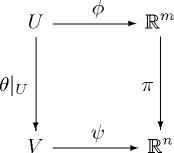
3. The diagram

   

   commutes, where [math]\displaystyle{ \pi : \mathbb{R}^m = \mathbb{R}^n \times \mathbb{R}^{m-n} \rightarrow \mathbb{R}^n\! }[/math] is the canonical projection.

Proof

Since translations are diffeomorphisms of [math]\displaystyle{ \mathbb{R}^k\! }[/math] for every [math]\displaystyle{ k \in \mathbb{N}\! }[/math], it is trivial to find charts [math]\displaystyle{ \phi_0 : U_0 \rightarrow U_0' \subset \mathbb{R}^m\! }[/math] and [math]\displaystyle{ \psi : V \rightarrow V' \subset \mathbb{R}^m\! }[/math] such that [math]\displaystyle{ \phi(p) = 0 \in \mathbb{R}^m\! }[/math] and [math]\displaystyle{ \psi(\theta(p)) = 0 \in \mathbb{R}^n\! }[/math]. Furthermore, since [math]\displaystyle{ V\! }[/math] is open, [math]\displaystyle{ U_0\! }[/math] is open and [math]\displaystyle{ \theta\! }[/math] is continuous, [math]\displaystyle{ U_0 \cap \theta^{-1}\left(V\right) \subset M\! }[/math] is open so that we may assume [math]\displaystyle{ U_0 \subset \theta^{-1}\left(V\right)\! }[/math] without loss of generality.

Let [math]\displaystyle{ \theta_0 = \psi \circ \theta \circ \phi_0^{-1} : U_0' \rightarrow V'\! }[/math] be the local representative of [math]\displaystyle{ \theta\! }[/math] and let [math]\displaystyle{ D_0 : \mathbb{R}^m \rightarrow \mathbb{R}^n \! }[/math] be the local representative of [math]\displaystyle{ d\theta_p\! }[/math]. Since [math]\displaystyle{ d\theta_p\! }[/math] is onto, we may apply a change of basis [math]\displaystyle{ T : \mathbb{R}^m \rightarrow \mathbb{R}^m }[/math] such that [math]\displaystyle{ D_0 = T^{-1} \circ \pi \circ T }[/math].

Let [math]\displaystyle{ \phi_1 = T \circ \phi_0\! }[/math]. Then [math]\displaystyle{ \phi_1\! }[/math] is a chart because [math]\displaystyle{ T\! }[/math] is a diffeomorphism. Let [math]\displaystyle{ \theta_1 = \psi \circ \theta \circ \phi_1^{-1} : U_0' \rightarrow V'\! }[/math] be the corresponding local representative, define [math]\displaystyle{ \zeta : U_0' \rightarrow \mathbb{R}^m\! }[/math] by [math]\displaystyle{ \zeta(x,y) = (\theta_1(x,y),y)\! }[/math], and let [math]\displaystyle{ D_1 : \mathbb{R}^m \rightarrow \mathbb{R}^n\! }[/math] be the differential of [math]\displaystyle{ \theta_1\! }[/math] at [math]\displaystyle{ 0\! }[/math]. Then, by construction of [math]\displaystyle{ T\! }[/math] we have that [math]\displaystyle{ D_1 = \pi\! }[/math] and hence [math]\displaystyle{ d \zeta_0 = \mathrm{id}_{\mathbb{R}^m}\! }[/math], which is invertible. Hence, the inverse function gives the existence of non-empty open set [math]\displaystyle{ U' \subset \zeta(U_1')\! }[/math] such that [math]\displaystyle{ \zeta|_{\zeta^{-1}(U')}\! }[/math] is a diffeomorphism. Put [math]\displaystyle{ U = \phi_1^{-1}(\zeta^{-1}(U'))\! }[/math] and [math]\displaystyle{ \phi = \zeta \circ \phi_1|_U\! }[/math]. Then [math]\displaystyle{ \phi\! }[/math] is a chart.

It remains to check that [math]\displaystyle{ \pi \circ \phi = \psi \circ \theta|_U\! }[/math], but this is clear: if [math]\displaystyle{ (x,y) = \phi_1(q)\! }[/math] for some [math]\displaystyle{ q \in U\! }[/math], then [math]\displaystyle{ \pi\circ\phi(q) = \pi\circ\zeta(x,y) = \theta_1(x,y) = \psi(\theta(q))\! }[/math] by definition of [math]\displaystyle{ \theta_1\! }[/math]. [math]\displaystyle{ \Box\! }[/math]