0708-1300/Class notes for Tuesday, September 11: Difference between revisions

From Drorbn
Jump to navigationJump to search
Line 53: Line 53:


'''Def:''' We say that <math>f</math> is differentiable (''diffable'') if there is a linear map <math>L</math> so that
'''Def:''' We say that <math>f</math> is differentiable (''diffable'') if there is a linear map <math>L</math> so that
<math>\lim_{h\rightarrow0}\frac{\right\|f(x+h)-f(x)-L(h)\left\|}{\right\|h\left\|}</math>
<math>\lim_{h\rightarrow0}</math>

Revision as of 15:26, 11 September 2007

0708-1300/Navigation Panel  
0708-1300-ClassPhoto.jpg
Add your name / see who's in!
# Week of... Links
Fall Semester
1 Sep 10 About, Tue, Thu
2 Sep 17 Tue, HW1, Thu
3 Sep 24 Tue, Photo, Thu
4 Oct 1 Questionnaire, Tue, HW2, Thu
5 Oct 8 Thanksgiving, Tue, Thu
6 Oct 15 Tue, HW3, Thu
7 Oct 22 Tue, Thu
8 Oct 29 Tue, HW4, Thu, Hilbert sphere
9 Nov 5 Tue,Thu, TE1
10 Nov 12 Tue, Thu
11 Nov 19 Tue, Thu, HW5
12 Nov 26 Tue, Thu
13 Dec 3 Tue, Thu, HW6
Spring Semester
14 Jan 7 Tue, Thu, HW7
15 Jan 14 Tue, Thu
16 Jan 21 Tue, Thu, HW8
17 Jan 28 Tue, Thu
18 Feb 4 Tue
19 Feb 11 TE2, Tue, HW9, Thu, Feb 17: last chance to drop class
R Feb 18 Reading week
20 Feb 25 Tue, Thu, HW10
21 Mar 3 Tue, Thu
22 Mar 10 Tue, Thu, HW11
23 Mar 17 Tue, Thu
24 Mar 24 Tue, HW12, Thu
25 Mar 31 Referendum,Tue, Thu
26 Apr 7 Tue, Thu
R Apr 14 Office hours
R Apr 21 Office hours
F Apr 28 Office hours, Final (Fri, May 2)
Register of Good Deeds
Errata to Bredon's Book
Announcements go here

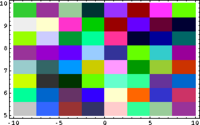
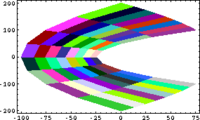
In Small Scales, Everything's Linear

06-240-QuiltBeforeMap.png 06-240-QuiltAfterMap.png

Code in Mathematica: 

QuiltPlot[{f_,g_}, {x_, xmin_, xmax_, nx_}, {y_, ymin_, ymax_, ny_}] :=
Module[
  {dx, dy, grid, ix, iy},
  SeedRandom[1];
  dx=(xmax-xmin)/nx;
  dy=(ymax-ymin)/ny;
  grid = Table[
    {x -> xmin+ix*dx, y -> ymin+iy*dy},
    {ix, 0, nx}, {iy, 0, ny}
  ];
  grid = Map[({f, g} /. #)&, grid, {2}];
  Show[
    Graphics[Table[
      {
        RGBColor[Random[], Random[], Random[]],
        Polygon[{
          grid[[ix, iy]],
          grid[[ix+1, iy]],
          grid[[ix+1, iy+1]],
          grid[[ix, iy+1]]
        }]
      },
      {ix, nx}, {iy, ny}
    ]],
    Frame -> True
  ]
]

QuiltPlot[{x, y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
QuiltPlot[{x^2-y^2, 2*x*y}, {x, -10, 10, 8}, {y, 5, 10, 8}]

See also 06-240/Linear Algebra - Why We Care.

Class Notes

Let and be two normed finite dimensional vector spaces and let be a function defined on a neighborhood of the point

Def: We say that is differentiable (diffable) if there is a linear map so that

Retrieved from "https://drorbn.net/index.php?title=0708-1300/Class_notes_for_Tuesday,_September_11&oldid=5354"