0708-1300/Class notes for Tuesday, September 11: Difference between revisions
From Drorbn
Jump to navigationJump to search
m (Class notes for Tuesday, September 11 moved to 0708-1300/Class notes for Tuesday, September 11) |
|||
| Line 50: | Line 50: | ||
==Class Notes== |
==Class Notes== |
||
Let $f:V\rightarrow W$ be a function defined in a neighborhood of the point $x$ |
|||
Revision as of 15:20, 11 September 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In Small Scales, Everything's Linear
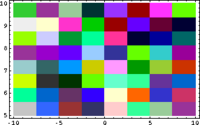
|
[math]\displaystyle{ \longrightarrow }[/math] | 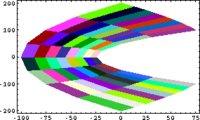
|
| [math]\displaystyle{ z }[/math] | [math]\displaystyle{ \mapsto }[/math] | [math]\displaystyle{ z^2 }[/math] |
Code in Mathematica:
QuiltPlot[{f_,g_}, {x_, xmin_, xmax_, nx_}, {y_, ymin_, ymax_, ny_}] :=
Module[
{dx, dy, grid, ix, iy},
SeedRandom[1];
dx=(xmax-xmin)/nx;
dy=(ymax-ymin)/ny;
grid = Table[
{x -> xmin+ix*dx, y -> ymin+iy*dy},
{ix, 0, nx}, {iy, 0, ny}
];
grid = Map[({f, g} /. #)&, grid, {2}];
Show[
Graphics[Table[
{
RGBColor[Random[], Random[], Random[]],
Polygon[{
grid[[ix, iy]],
grid[[ix+1, iy]],
grid[[ix+1, iy+1]],
grid[[ix, iy+1]]
}]
},
{ix, nx}, {iy, ny}
]],
Frame -> True
]
]
QuiltPlot[{x, y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
QuiltPlot[{x^2-y^2, 2*x*y}, {x, -10, 10, 8}, {y, 5, 10, 8}]
See also 06-240/Linear Algebra - Why We Care.
Class Notes
Let $f:V\rightarrow W$ be a function defined in a neighborhood of the point $x$
