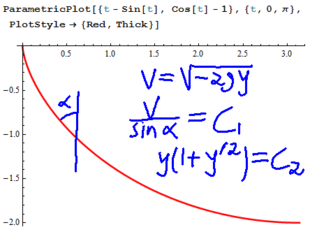12-267: Difference between revisions

From Drorbn
Jump to navigationJump to search
No edit summary
No edit summary
 
(42 intermediate revisions by 10 users not shown)
Line 24: Line 24:
{{Template:12-267:Dror/Students Divider}}
{{Template:12-267:Dror/Students Divider}}


[[User:Drorbn|Drorbn]] 06:36, 12 September 2012 (EDT): Material by [[User:Syjytg|Syjytg]] moved to [[12-267/Tuesday September 11 Notes]].
===Solving the complicated integral in the Brachistochroe integral===


[http://imgur.com/a/OSx1U#0 Summary of techniques to solve differential equations] [[User:Vsbdthrsh|Vsbdthrsh]]
integral sqrt((d-y)/y) dy

= integral sqrt(d y-y^2)/y dy
[[12-267/Existence_And_Uniqueness_Theorem|Fundamental Theorem and Proof from Lecture]] [[User:Twine|Twine]]
For the integrand sqrt(d y-y^2)/y, complete the square:

= integral sqrt(d^2/4-(y-d/2)^2)/y dy
[[12-267/Derivation_of_Euler-Lagrange|Derivation of Euler-Lagrange from Lecture]] [[User:Twine|Twine]]
For the integrand sqrt(d^2/4-(y-d/2)^2)/y, substitute u = y-d/2 and du = dy:

= integral (2 sqrt(d^2/4-u^2))/(d+2 u) du
[http://graphics.ethz.ch/teaching/former/vc_master_06/Downloads/viscomp-varcalc_6.pdf Useful PDF: proof of Euler-Lagrange equation, explanation, examples ] [[User:Vsbdthrsh|Vsbdthrsh]]
= 2 integral sqrt(d^2/4-u^2)/(d+2 u) du

For the integrand sqrt(d^2/4-u^2)/(d+2 u), (assuming all variables are positive) substitute u = 1/2 d sin(s) and du = 1/2 d cos(s) ds. Then sqrt(d^2/4-u^2) = sqrt(d^2/4-1/4 d^2 sin^2(s)) = 1/2 d cos(s) and s = sin^(-1)((2 u)/d):
12-267 [http://math.hunter.cuny.edu/mbenders/cofv.pdf In-depth coverage of Calculus of Variations][[User:Simon1|Simon1]]
= d^2/2 integral (cos^2(s))/(d sin(s)+d) ds

For the integrand (cos^2(s))/(d sin(s)+d), substitute p = tan(s/2) and dp = 1/2 sec^2(s/2) ds. Then transform the integrand using the substitutions sin(s) = (2 p)/(p^2+1), cos(s) = (1-p^2)/(p^2+1) and ds = (2 dp)/(p^2+1):
12-267 [http://highered.mcgraw-hill.com/sites/dl/free/007063419x/392340/Calculus_of_Variations.pdf A good summary of Calculus of Variations]
= d^2/2 integral (2 (1-p^2)^2)/((p^2+1)^3 ((2 d p)/(p^2+1)+d)) dp
[[User:Simon1|Simon1]]
Simplify the integrand (2 (1-p^2)^2)/((p^2+1)^3 ((2 d p)/(p^2+1)+d)) to get (2 (p-1)^2)/(d p^4+2 d p^2+d):

= d^2/2 integral (2 (p-1)^2)/(d p^4+2 d p^2+d) dp
12-267 [http://imgur.com/a/1vy11#0 All class notes from September 10th to October 5th] [[User:Simon1|Simon1]]
= d^2 integral (p-1)^2/(d p^4+2 d p^2+d) dp

= d^2 integral (p-1)^2/(d (p^2+1)^2) dp
12-267 [http://imgur.com/a/uLSlM Summary of Numerical Methods] [[User:Simon1|Simon1]]
= d integral (p-1)^2/(p^2+1)^2 dp

For the integrand (p-1)^2/(p^2+1)^2, use partial fractions:
[[12-267/Numerical_Methods|Numerical Methods (wiki)]] [[User:Twine|Twine]]
= d integral (1/(p^2+1)-(2 p)/(p^2+1)^2) dp

= d integral 1/(p^2+1) dp-2 d integral p/(p^2+1)^2 dp
12-267 [http://imgur.com/a/tliYg Summary of Chapter 3 from the Textbook on Constant Coefficient Second Order ODEs] [[User:Simon1|Simon1]]
For the integrand p/(p^2+1)^2, substitute w = p^2+1 and dw = 2 p dp:

= d integral 1/(p^2+1) dp-d integral 1/w^2 dw
Past exams from [http://exams.library.utoronto.ca.myaccess.library.utoronto.ca/handle/exams/4429 December 2009] and [http://exams.library.utoronto.ca.myaccess.library.utoronto.ca/handle/exams/4429 December 2010] [[User:Twine|Twine]]
The integral of 1/(p^2+1) is tan^(-1)(p):

= d tan^(-1)(p)-d integral 1/w^2 dw
Handwritten notes by [[User:Ktnd3|Ktnd3]]:
= d tan^(-1)(p)+d/w+constant

Substitute back for w = p^2+1:
* September: [[Media:Mat267_-_lecture_1(sep.10).PDF|10th]], [[Media:Mat267_-_lecture_2%28sep.11%29.PDF|11th]], [[Media:Mat267_-_lecture_3%28sep.14%29.PDF|14th]], [[Media:Mat267_-_lecture_4%28sep.17%29.PDF|17th]], [[Media:12-267%28lecture5%29.PDF|18th]], [[Media:12-267%28lecture6%29.PDF|21st]], [[Media:12-267%28lecture7%29.PDF|24th]], [[Media:12-267%28lecture8%29.PDF|25th]], [[Media:12-267%28lecture9%29.PDF|28th]]
= (d ((p^2+1) tan^(-1)(p)+1))/(p^2+1)+C

Substitute back for p = tan(s/2):
* October: [[Media:12-267%28lecture10%29.PDF|1st]], [[Media:12-267%28lecture11%29.PDF|2nd]], [[Media:12-267%28lecture12%29.PDF|5th]], [[Media:12-267%28lecture13%29.PDF|9th]] [[Media:12-267%28lecture14%29.PDF|12th]]
= 1/2 d (cos(s)+2 tan^(-1)(tan(s/2))+1)+C

Substitute back for s = sin^(-1)((2 u)/d):
[http://i.imgur.com/uTugV.jpg Quick guide: system of 1st order linear equations] [[User:Vsbdthrsh|Vsbdthrsh]]
= 1/2 (sqrt(d^2-4 u^2)+2 d tan^(-1)((2 u)/(d (sqrt(1-(4 u^2)/d^2)+1)))+d)+C

Substitute back for u = y-d/2:
Help of Inverse Matrix [http://mathworld.wolfram.com/MatrixInverse.html Matrix Inverse] [[User:Dongwoo.kang|Dongwoo.kang]]
= d (-tan^(-1)((d-2 y)/(2 d sqrt((y (d-y))/d^2)+d)))+sqrt(y (d-y))+d/2+C

Factor the answer a different way:
12-267 [http://imgur.com/a/50sRR All class notes from October 5th to October 30th] [[User:Simon1|Simon1]]
= 1/2 (-2 d tan^(-1)((d-2 y)/(2 d sqrt((y (d-y))/d^2)+d))+2 sqrt(y (d-y))+d)+C

Which is equivalent for restricted y and d values to:
[http://imgur.com/a/sZSYx#0 Quick guide: Power Series + ODE] [[User:Vsbdthrsh|Vsbdthrsh]]
= y sqrt(d/y-1)-1/2 d tan^(-1)((sqrt(d/y-1) (d-2 y))/(2 (d-y)))+C [[User:Syjytg|Syjytg]] 23:00, 11 September 2012 (EDT)

[https://lh4.googleusercontent.com/-V1WnvvzXRlE/TxTGwl_BBjI/AAAAAAAAE9k/yVuy1zRmnWs/Gatos-cute-cute-32-800x500.jpg Mirrors do actually flip top-to-bottom, depending on how you look at them] [[User:jonathanrlove|jonathanrlove]]

[http://www.guardian.co.uk/notesandqueries/query/0,5753,-19877,00.html Actually, mirrors don't flip top-to-bottom *or* left-to-right] [[User:Twine|Twine]]

[[12-267/Topic_List|Topics covered this semester]] - [[User:Twine|Twine]]

(Summary of ODE) Hope it is Helpful.
[[Media:12-267(ODE-Summary).pdf]] - [[User:Dongwoo.kang|Dongwoo.kang]]

[[Media:12-267-ODE_to_Joy.pdf|A full exposition on most of the topics covered]] [[User:Samer|Samer]]

Latest revision as of 20:41, 17 December 2012


DBN: Classes: 2012-13: 12-267 / Navigation
Additions to this web site no longer count towards good deed points.
# Week of... Notes and Links
1 Sep 10 About This Class. dbnvp Monday: Introduction and the Brachistochrone. dbnvp Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. dbnvp Friday: Some basic techniques: first order linear equations.
2 Sep 17 dbnvp Monday: Separated equations, escape velocities. HW1. dbnvp Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. dbnvp Friday: Reverse engineering separated and exact equations.
3 Sep 24 dbnvp Monday: Solving exact equations, integration factors. HW2. dbnvp Tuesday: Statement of the Fundamental Theorem. Class Photo. dbnvp Friday: Proof of the Fundamental Theorem.
4 Oct 1 dbnvp Monday: Last notes on the fundamental theorem. HW3. dbnvp Tuesday Hour 1: The chain law, examples of variational problems. dbnvp Tuesday Hour 2: Deriving Euler-Lagrange. dbnvp Friday: Reductions of Euler-Lagrange.
5 Oct 8 Monday is thanksgiving. dbnvp Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. dbnvp Friday: More Lagrange multipliers, numerical methods.
6 Oct 15 dbnvp Monday: Euler and improved Euler. dbnvp Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. dbnvp Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
7 Oct 22 dbnvp Monday: Multiple roots, reduction of order, undetermined coefficients. dbnvp Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
8 Oct 29 dbnvp Monday: The basic properties of matrix exponentiation. dbnvp Tuesday: Matrix exponentiation: examples. dbnvp Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
9 Nov 5 dbnvp Monday: Non-homogeneous systems. dbnvp Tuesday: The Catalan numbers, power series, and ODEs. dbnvp Friday: Global existence for linear ODEs, the Wronskian.
10 Nov 12 Monday-Tuesday is UofT November break. HW7. dbnvp Friday: Series solutions for .
11 Nov 19 dbnvp Monday: is irrational, more on the radius of convergence. dbnvp Tuesday (class): Airy's equation, Fuchs' theorem. dbnvp Tuesday (tutorial): Regular singular points. HW8. dbnvp Friday: Discussion of regular singular points..
12 Nov 26 dbnvp Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). dbnvp Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. dbnvp Friday: Non-oscillation, Sturm comparison.
13 Dec 3 dbnvp Monday: More Sturm comparisons, changing the independent variable. dbnvp Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
F1 Dec 10
F2 Dec 17 The Final Exam (time, place, style, office hours times)
Register of Good Deeds
12-267-ClassPhoto.jpg
Add your name / see who's in!
12-267-Splash.png

Advanced Ordinary Differential Equations

Department of Mathematics, University of Toronto, Fall 2012

Agenda: If calculus is about change, differential equations are the equations governing change. We'll learn much about these, and nothing's more important!

Instructor: Dror Bar-Natan, drorbn@math.toronto.edu, Bahen 6178, 416-946-5438. Office hours: by appointment.

Classes: Mondays, Tuesdays, and Fridays 9-10 in RW 229.

Teaching Assistant
 Teaching Assistant: Jordan Bell, jordan.bell@utoronto.ca.

Tutorials: Tuesdays 10-11 at RW 229. No tutorials on the first week of classes.

Text

Boyce and DiPrima, Elementary Differential Equations and Boundary Value Problems (current edition is 9th and 10th will be coming out shortly. Hopefully any late enough edition will do).

Further Resources

  • Also previously taught by T. Bloom, C. Pugh, D. Remenik.
Dror's notes above / Student's notes below

Drorbn 06:36, 12 September 2012 (EDT): Material by Syjytg moved to 12-267/Tuesday September 11 Notes.

Summary of techniques to solve differential equations Vsbdthrsh

Fundamental Theorem and Proof from Lecture Twine

Derivation of Euler-Lagrange from Lecture Twine

Useful PDF: proof of Euler-Lagrange equation, explanation, examples Vsbdthrsh

12-267 In-depth coverage of Calculus of VariationsSimon1

12-267 A good summary of Calculus of Variations Simon1

12-267 All class notes from September 10th to October 5th Simon1

12-267 Summary of Numerical Methods Simon1

Numerical Methods (wiki) Twine

12-267 Summary of Chapter 3 from the Textbook on Constant Coefficient Second Order ODEs Simon1

Past exams from December 2009 and December 2010 Twine

Handwritten notes by Ktnd3:

Quick guide: system of 1st order linear equations Vsbdthrsh

Help of Inverse Matrix Matrix Inverse Dongwoo.kang

12-267 All class notes from October 5th to October 30th Simon1

Quick guide: Power Series + ODE Vsbdthrsh

Mirrors do actually flip top-to-bottom, depending on how you look at them jonathanrlove

Actually, mirrors don't flip top-to-bottom *or* left-to-right Twine

Topics covered this semester - Twine

(Summary of ODE) Hope it is Helpful. Media:12-267(ODE-Summary).pdf - Dongwoo.kang

A full exposition on most of the topics covered Samer

Retrieved from "https://drorbn.net/index.php?title=12-267&oldid=12878"