06-1350/Homework Assignment 4
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due on Tuesday, December 5 2006.
This is an unusual assignment; the task at hand is to do some real research, stuff that to the best of my knowledge had never been done before and most definitely was never written up. Thus the rules will also be a bit different - your work (or at least the accumulation of work on this topic by everyone in class) is meant to be used and useful. So it must be presented in a very readable form (i.e., typed up and with figures) and it must be reliable; in fact, it will be computer verifiable. But some rules will be relaxed, as well.
The task is a bit technical. But hey, it is a homework assignment, after all!
The Task
Write all the relations between , , and in a completely explicit way, both as formulas and as illuminating figures, and then do the same to all the syzygies between these relations. Finally, enter everything you have written into a Mathemmatica script that will verify that for the complex you have created, .
Note that when I write "all relations" or "all syzygies" above I really mean "a complete independent set of relations/syzygies". And while this cannot be formalized, the prettier your representatives are, the better!
The Rules
The first relation and the first syzygy were written by Dror (see below or visit User:Drorbn/06-1350-HW4). You are to copy his work into your user space and complete it there.
- On this wiki create a page named "User:YourUsernameHere/06-1350-HW4" (or simply "User:YourUsernameHere/HW4"). If necessary, go to Help:Contents to see how this is done.
- Copy User:Drorbn/06-1350-HW4 into your page. The easiest way to do that is to edit User:Drorbn/06-1350-HW4 and copy the source code into your page using copy-paste on your windowing system. Then "preview" or "save" your copy but "cancel" the edit to User:Drorbn/06-1350-HW4.
- Now work on your page...
- Copying is legal! You are allowed, indeed encouraged, to collaborate with others or to simply copy results from other people's pages into yours. The goal is to get something complete. If one of you will start with something incomplete and somebody else will do some other incomplete thing and yet another person will merge the two, we may achieve the goal.
- If you copy, always credit the original source! Likewise, if I will ever use any of the material that will be first produced here, I am committed to crediting the source(s).
- You will get a good though not perfect grade on this assignment for doing anything at all, or even for doing nothing at all but copying on the understanding that by submitting your work you are testifying that you understand it. Perfect grades will go to the people who will make substantial contributions.
- Elegance counts! Beauty counts! A systematic approach counts!
A Bonus Question
Find the definitive completion of the silliest proof for the existence of exponentials. In other words, find the definitive proof that if is a two-variable power series for which , the there exists a single-variable power series for which .
User:Drorbn/06-1350-HW4
The Generators
Our generators are , , and :
| Picture | 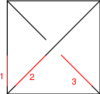
|
||||
| Generator | |||||
| Perturbation |
The Relations
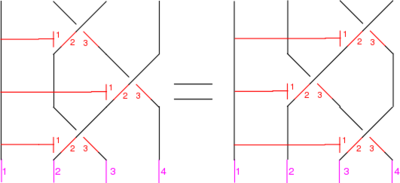
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
Linearized and written in functional form, this becomes
The Syzygies
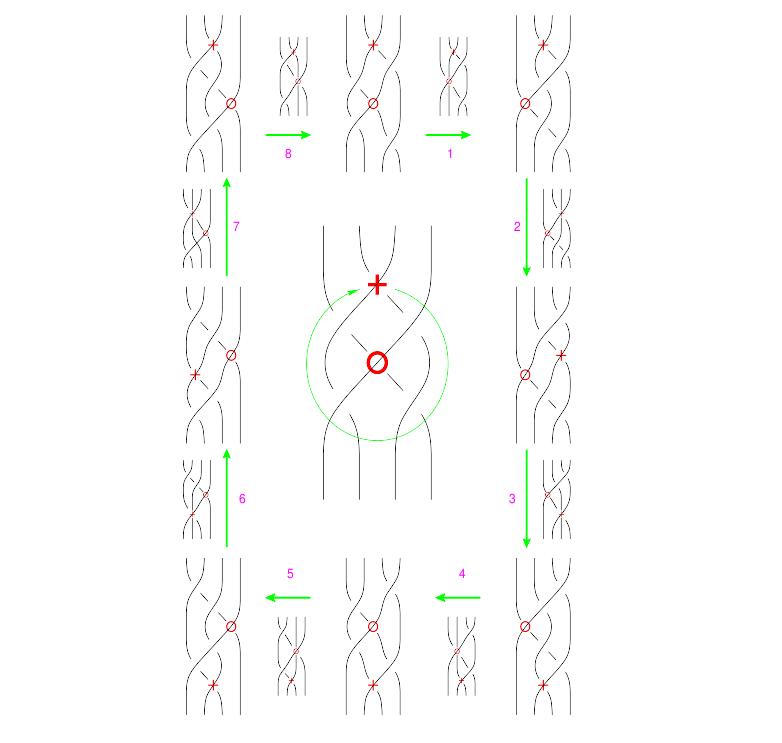
The "B around B" Syzygy
The picture, with all shielding removed, is
| (Drawn with Inkscape) (note that lower quality pictures are also acceptable) |
The functional form of this syzygy is
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|
Links
In order to make it easier for us to see each others work, and not all work on the same parts of the assignment I suggest that you can link here to your assignment page. You can also say what you have worked out there and what you are planing on working on.
My page is User:Jana/06-1350-HW4
User:zsuzsi/HW4 (worked out some relations and copied Andy's work)
User:Karenechu/06-1350-HW4 (posted an attempt on the unzip operation, problem with the delete operation and copied Suzsi's and Andy's work)