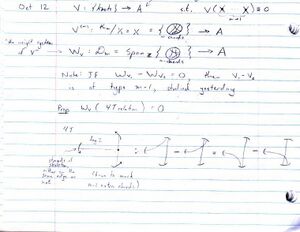06-1350/Class Notes for Thursday October 12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
A Question
Determine the image of the differential operator
acting on polynomials in the variables , and . More precisely - determine the quotient of the space of polynomials in , and by the image of . More generally, it is a standard subject in algebra to deal with the images and cokernels of algebraic operators; the results are ideals and the quotients are often-studied algebras. But where's the theory for the images and "cokernels" of differential operators.
Why do I care?
The answer to this question is directly related to the determination of the "envelope" of the Alexander polynomial for two component links.
Some Computations
The following table (taken from [Bar-Natan_95] and [Kneissler_97]) shows the number of type invariants of knots and framed knots modulo type invariants ( and ) and the number of multiplicative generators of the algebra in degree () for . Some further tabulated results are in [Bar-Natan_96].
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 0 | 1 | 1 | 3 | 4 | 9 | 14 | 27 | 44 | 80 | 132 | 232 | |
| 1 | 1 | 2 | 3 | 6 | 10 | 19 | 33 | 60 | 104 | 184 | 316 | 548 | |
| 0 | 1 | 1 | 1 | 2 | 3 | 5 | 8 | 12 | 18 | 27 | 39 | 55 |
Some Further Computations
Some further computations for links and tangles were made by Siddarth Sankaran and Zavosh Amir-Khosravi. See VasCalc Results - ChordMod4T.
Some Bounds
Little is known about these dimensions for large . There is an explicit conjecture in [Broadhurst_97] but no progress has been made in the direction of proving or disproving it. The best asymptotic bounds available are:
Theorem. For large , (for any fixed , see [Dasbach_00], [Kontsevich]) and ([Stoimenow_98], [Zagier_01]).
Some References
[Bar-Natan_95] ^ D. Bar-Natan, On the Vassiliev knot invariants, Topology 34 (1995) 423-472.
[Bar-Natan_96] ^ D. Bar-Natan, Some computations related to Vassiliev invariants, electronic publication, http://www.math.toronto.edu/~drorbn/LOP.html#Computations.
[Broadhurst_97] ^ D. J. Broadhurst, Conjectured enumeration of Vassiliev invariants, preprint, September 1997, arXiv:q-alg/9709031.
[Dasbach_00] ^ O. T. Dasbach, On the combinatorial structure of primitive Vassiliev invariants III - a lower bound, Comm. in Cont. Math. 2-4 (2000) 579-590, arXiv:math.GT/9806086.
[Kneissler_97] ^ J. A. Kneissler, The number of primitive Vassiliev invariants up to degree twelve, preprint, June 1997, arXiv:q-alg/9706022.
[Kontsevich] ^ M. Kontsevich, unpublished.
[Stoimenow_98] ^ A. Stoimenow, Enumeration of chord diagrams and an upper bound for Vassiliev invariants, Jour. of Knot Theory and its Ramifications 7(1) (1998) 94-114.
[Zagier_01] ^ D. Zagier, Vassiliev invariants and a strange identity related to the Dedekind eta-function, Topology 40(5) (2001) 945-960.