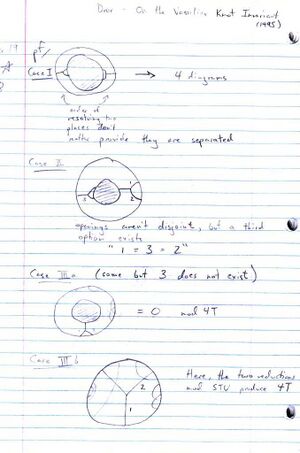
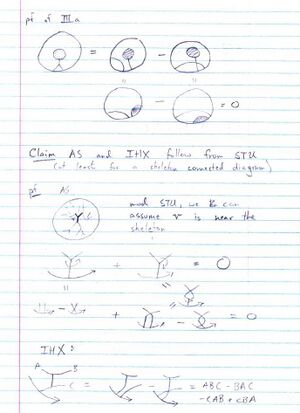
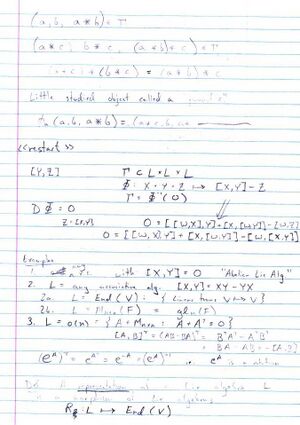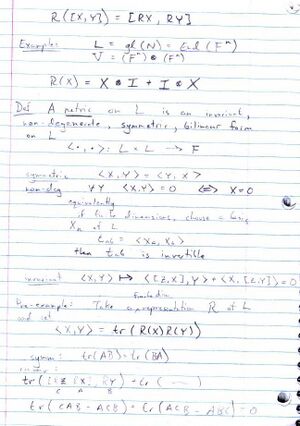06-1350/Class Notes for Thursday October 19

06-1350/Navigation Panel   # Week of... Links 1 Sep 11 About, Tue, Thu 2 Sep 18 Tue, Kurlin(P), Thu 3 Sep 25 Tue, Photo, Thu 4 Oct 2 HW1, Tue, Thu 5 Oct 9 Tue(P), Thu(P) 6 Oct 16 HW2, Tue(P), Thu(P) 7 Oct 23 Tue(P), Thu 8 Oct 30 HW3, Tue, Thu 9 Nov 6 Tue ($\nu$), Thu 10 Nov 13 Tue, Thu 11 Nov 20 HW4(P), Thu 12 Nov 27 Thu 13 Dec 4 Syzygies in Asymptote, Final Jan 8 Grades Note. (P) means "contains a problem that Dror cares about". Add your name / see who's in! On to 07-1352

Matrix exponentiation is harder than you think

You think you know matrix exponentiation? OK, here's a question to test your knowledge. Fix a natural number $n$. From here and on the word "matrix" means "an $n\times n$ matrix with rational entries". Let $W$ be a linear combination of words whose letters are either matrices $M_i$ or meaningless symbols of the form $\exp(h_jM_i)$. Say that $W\sim 0$ if $W$ becomes $0$ when it is interpreted as a sum of products of formal power series of matrices and polynomials in formal variables $h_j$, where $\exp(h_jM_i)$ is interpreted to mean $\sum_{k=0}^\infty\frac{M_i^kh_j^k}{k!}$. (Note that the number of formal parameters $h_j$ need not equal the number of matrices involved).

Thus for example, if the matrices $M_1$ and $M_2$ are known to commute (say $M_1=\begin{pmatrix}1&0\\0&0\end{pmatrix}$ and $M_2=\begin{pmatrix}0&0\\0&1\end{pmatrix}$), then $\exp(hM_1)\exp(hM_2)-\exp(hM_2)\exp(hM_1)\sim 0$. In fact, it is even true that $\exp(h_1M_1)\exp(h_2M_2)-\exp(h_2M_2)\exp(h_1M_1)\sim 0$.

Question. Provide a reasonable algorithm to decide if $W\sim 0$ or not. In other words, provide a reasonable algorithm to decide if a certain equality between rational matrices and their exponentials holds or not.

Note that an unreasonable algorithm for this question is readily available. Over the algebraic closure of ${\mathbb Q}$, exponentiations such as $\exp(h_jM_i)$ can be carried out explicitly using diagonalization, and then matrices can be multiplied or added as required, and the question is settled. The reason this is unreasonable is that the algebraic closure of ${\mathbb Q}$ is easy to speak of but very hard to work with. Many of you must have seen computer programs that manipulate rational numbers; this is easy. Have you ever seen a computer program that manipulates arbitrary algebraic numbers?

And of course, I could have asked the question about matrices with entries in some ring that doesn't have an algebraic closure. The question still makes sense, but the approach with explicit exponentiation does not.

In reality I care about an analog of this question in which the underlying algebra isn't necessarily a matrix algebra. For any algebra $A$ and any $M\in A$, $\exp(hM)$ makes sense within the algebra $A[[h]]$ of formal power series in $h$ with coefficients in $A$. Hence our question makes sense even if $A$ isn't a matrix algebra.

Note. As of the morning of October 19, I actually know how to solve this question. Whether my solution is useful or not, whether I will be able to use it or not, and if not useful, whether I will be able to make a precise sense of the way it is not useful, is yet to be seen. --Drorbn 07:36, 19 October 2006 (EDT)

Scanned Notes