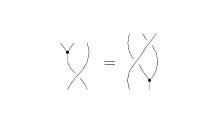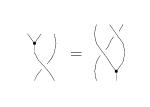The Generators
Our generators are  ,
,  ,
,  and
and  :
:
| Picture
|
|
|

|
|
|
| Generator
|

|

|

|

|

|
| Perturbation
|

|

|

|

|

|
The Relations
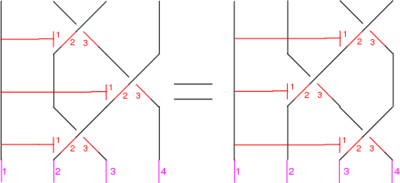
The Reidemeister Move R2 (Andy's)
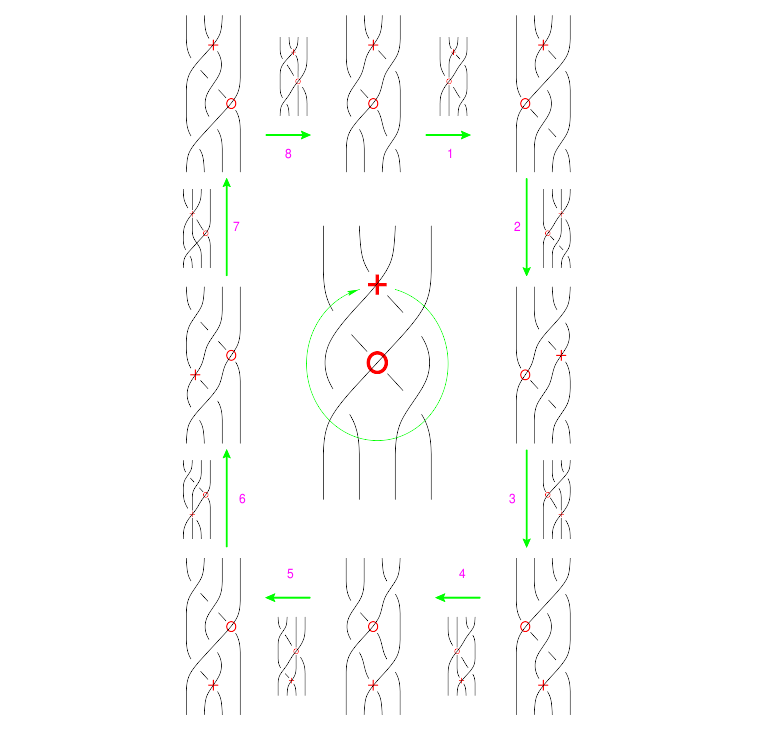
The following version of R2 was the easiest to use to build my original  around
around  syzygy:
syzygy:
In formulas, this is

Linearized and written in functional form, this becomes

|
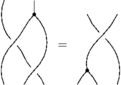
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|

|
|
|

|
R4
This Reidemeister move has a number of forms. I will put two here, both in linearized functional form. The two following were copied from Andy.
R4c
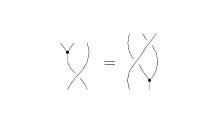

|

|
|
|

|
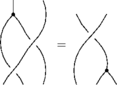
R4d
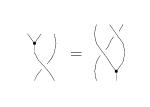

|

|
|
|

|
To establish the syzygy below, I needed two versions of R4. First:
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|
Second:
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|
Are these independent, or can they be shown to be equivalent using other relations?
The Syzygies
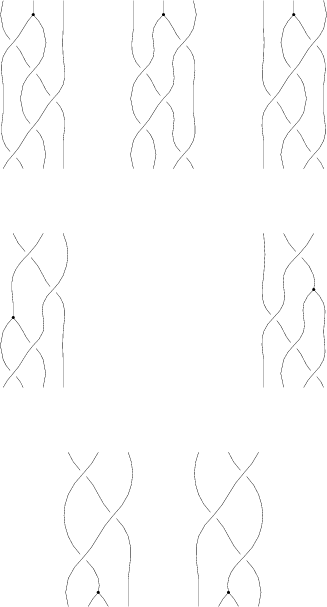
The "B around B" Syzygy
The picture, with all shielding removed, is
|
|
(Drawn with Inkscape)
(note that lower quality pictures are also acceptable)
|
The functional form of this syzygy is

|

|
|
|

|
|
|

|
The " around B" Syzygy (By Andy)
around B" Syzygy (By Andy)
The picture, with all shielding (and any other helpful notations) removed, is
The functional form of this syzygy is

|

|
|
|

|
|
|

|
Phi around Phi

A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy,  . Copy paste it into a live Mathematica session to see that it's right!
. Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|