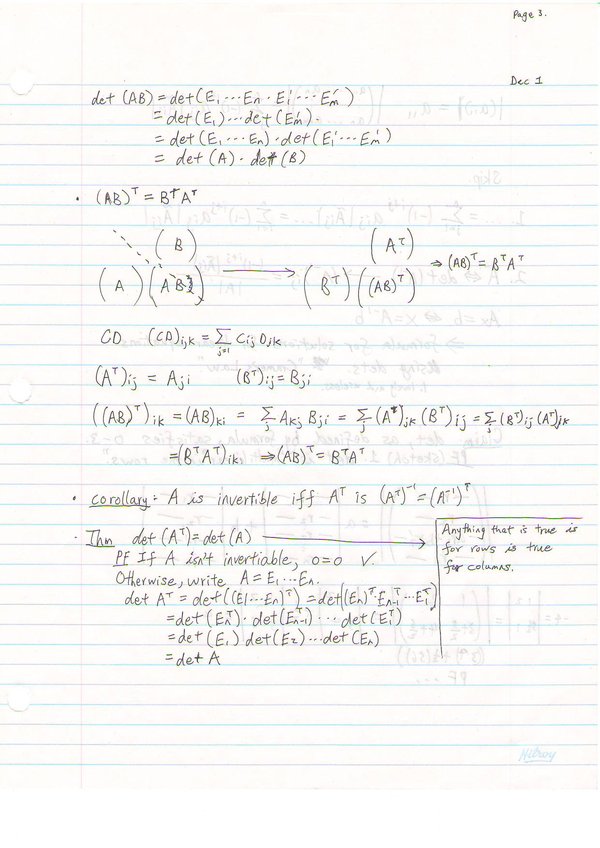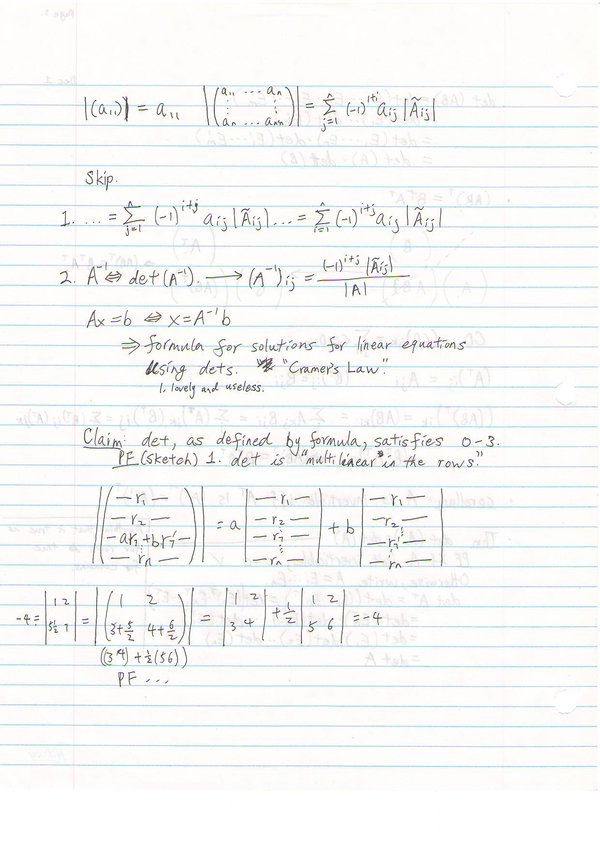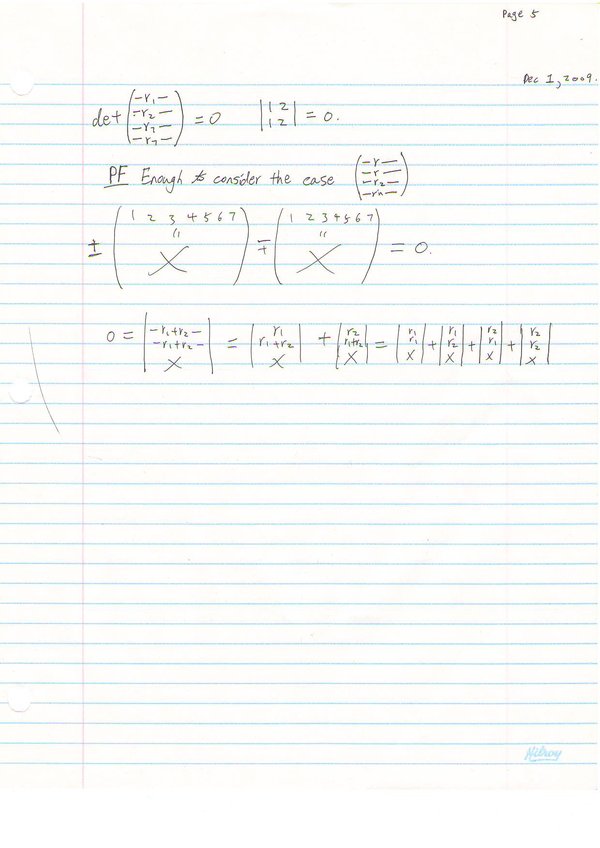09-240/Classnotes for Tuesday December 1

09-240/Navigation Panel   Additions to the MAT 240 web site no longer count towards good deed points # Week of... Notes and Links 1 Sep 7 Tue, About, Thu 2 Sep 14 Tue, HW1, HW1 Solution, Thu 3 Sep 21 Tue, HW2, HW2 Solution, Thu, Photo 4 Sep 28 Tue, HW3, HW3 Solution, Thu 5 Oct 5 Tue, HW4, HW4 Solution, Thu, 6 Oct 12 Tue, Thu 7 Oct 19 Tue, HW5, HW5 Solution, Term Test on Thu 8 Oct 26 Tue, Why LinAlg?, HW6, HW6 Solution, Thu 9 Nov 2 Tue, MIT LinAlg, Thu 10 Nov 9 Tue, HW7, HW7 Solution Thu 11 Nov 16 Tue, HW8, HW8 Solution, Thu 12 Nov 23 Tue, HW9, HW9 Solution, Thu 13 Nov 30 Tue, On the final, Thu S Dec 7 Office Hours F Dec 14 Final on Dec 16 To Do List The Algebra Song! Register of Good Deeds Misplaced Material Add your name / see who's in!

--- Wiki Format ---

MAT240 – December 1st

Basic Properties of det: M_nxn→F: 0 det(I) = 1

1. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle det(E'_{i,j\,\!}A) = -det(A) ; |E'_{i,j\,\!}|= -1. [Note: det(EA) = |E||A|]}

• Also, note that exchanging two rows flips the sign.

2. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle det(E^2_{i,c\,\!}A) = det(A) ; |E^2_{i,j,c\,\!}| = 1}

• These are "enough"!

3. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle det((E_{i,j,c\,\!}A) = det(A) ; |E^3_{i,j,c\,\!}| = 1}

• Adding a multiple of one row to another does not change the determinant.

The determinant of any matrix can be calculated using the properties above.

Theorem:

If $det':M_{nxn\,\!}$→F satisfies properties 0-3 above, then $det'=det$

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle det(A) = det'(A)}

Philosophical remark: Why not begin our inquiry with the properties above?

We must find an implied need for their use; thus, we must know whether a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle det} exists first.