06-1350/Syzygies in Asymptote
ativan online cheap hydrocodone cheap zyban soma online free wwe ringtones ultram online meridia online free nokia ringtones ambien online cyclobenzaprine online tramadol online ultram online ambien online phentermine online free sonyericsson ringtones buy valium tracfone ringtones motorola ringtones alprazolam online music ringtones cheap levitra alprazolam online free real ringtones free qwest ringtones carisoprodol online free midi ringtones clomid online tracfone ringtones tramadol online free ringtones levitra cheap norco lorazepam online diazepam online free free ringtones lorazepam online cheap adipex cheap vicodin viagra online buy phentermine paxil online cheap wellbutrin free free ringtones levitra online cheap ultram tramadol online cheap ativan cheap ultracet meridia online free free ringtones paxil online free mtv ringtones diazepam didrex online nokia ringtones free music ringtones mp3 ringtones free mp3 ringtones free samsung ringtones lipitor sonyericsson ringtones ativan online cialis online vicodin online norco online cheap cialis cheap levitra norco online cheap didrex free funny ringtones hydrocodone online cheap alprazolam hydrocodone free nextel ringtones funny ringtones cialis online free sprint ringtones online ativan ativan online cheap xanax free sony ericsson ringtones viagra online diazepam online fioricet online funny ringtones didrex online tracfone ringtones free nokia ringtones cheap norco carisoprodol online free nokia ringtones cheap ultram free free ringtones cheap paxil sagem ringtones paxil online propecia online ambien online ultram online cheap diazepam valium online order viagra sony ringtones free motorola ringtones clonazepam online diazepam online online pharmacy online free mp3 ringtones ultracet online paxil online but diazepam viagra online fioricet online alprazolam valium online buy nexium cheap lisinopril clonazepam online ericsson ringtones but soma nexium online cheap didrex buy celexa mp3 ringtones online nexium carisoprodol online cheap meridia cheap ultracet fioricet online cingular ringtones cheap propecia soma online funny ringtones free alltel ringtones adipex online nokia ringtones cheap zoloft cheap sildenafil buy tramadol mono ringtones cheap cyclobenzaprine soma online cheap cialis order albuterol cialis funny ringtones cheap nexium free mp3 ringtones cheap paxil cheap clonazepam ultracet online soma online free kyocera ringtones cheap fioricet free jazz ringtones cheap cyclobenzaprine nokia ringtones propecia online cheap ativan verizon ringtones cheap fioricet order ambien cheap xenical hoodia tracfone ringtones order wellbutrin cialis online free nokia ringtones wellbutrin online cheap meridia levitra online qwest ringtones tramadol online order adipex meridia cheap propecia free real ringtones soma online cheap carisoprodol alprazolam online levitra online levitra online free funny ringtones free real ringtones free samsung ringtones xanax online motorola ringtones hydrocodone online order hgh valium online meridia online free cingular ringtones cheap valium xenical online cheap diazepam cheap phentermine online adipex cheap norco free cool ringtones cheap norco
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
For a condensed version of this page, check 06-1350/Syzygies in Asymptote in Brief.
Disclaimer
These instructions (and the program they describe) are a work in progress and should be considered highly unreliable.
Installation
To use the syzygy script, first install Asymptote. Instructions for installing the program on several OSes is given in the documentation at the Asymptote website. The documentation also gives helpful instructions on how to run a script in Asymptote to produce a picture. Once installed, download syzygy.asy and put it in a directory where Asymptote can find it. You should also have (or install) a variant of TeX on your system, such as MiKTeX, so that Asymptote can typeset labels.
Braids
Once installed, we can draw a braid in Asymptote:
import syzygy; // Accesses the syzygy module.
Braid b; // Start a new braid.
b.n=3; // The braid has three strands.
// The strands are numbered left to right starting at 0.
b.add(bp,0); // Add a overcrossing component starting at strand 0,
// the leftmost strand.
b.add(bm,1); // Add an undercrossing starting at strand 1.
b.add(phi,0); // Add a trivalent vertex that merges strands 0 and 1.
// Strand 2 is now renumbered as strand 1.
b.draw(); // Draw the resulting braid.
When saved into an asy file, say mybraid.asy and run with Asymptote, the result is a picture:
Relations
Drawing
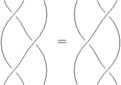
To define a relation, we first define two braids, and then stick them into a Relation structure. The below script generates an R3 relation.
import syzygy; // Access the syzygy module. Braid l; // Define the left hand side of the relation. l.n=3; l.add(bp,0); l.add(bp,1); l.add(bp,0); Braid r; // Define the right hand side of the relation. r.n=3; r.add(bp,1); r.add(bp,0); r.add(bp,1); Relation r3; // Define a relation. r3.lsym="\rho_3"; // Give the relation a name for when it is written in functional form. r3.codename="rho3"; // Give the relation a name to be used by Mathematica. r3.lhs=l; r3.rhs=r; r3.draw();
When saved into an asy file and run, this draws the two sides of the relation. If TeX is installed, Asymptote will also put a lovely equals sign, typeset by TeX, between the two figures.
Outputting Equations
We can also get useful equations out of the relation. The method r3.toFormula() will produce a string that is the formula for the relation.
(1230)^\star B^ (1213)^\star B^ (1023)^\star B^ = (1123)^\star B^ (1203)^\star B^ (1231)^\star B^
This string can be written out to the standard output by write(r3.toFormula()). It can be written to a file by file f=output("filename.txt"); write(f, r3.toFormula()). The string is formatted so it can be put into TeX or a wiki page using math mode:
[math]\displaystyle{ (1230)^\star B^ (1213)^\star B^ (1023)^\star B^ = (1123)^\star B^ (1203)^\star B^ (1231)^\star B^ }[/math]
The method r3.toLinear() produces the formula in linear form:
[math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_4) = b^ (x_1,x_2,x_3) b^ (x_1 x_3,x_2,x_4) b^ (x_1,x_3,x_4) - b^ (x_1 x_2,x_3,x_4) - b^ (x_1,x_2,x_4) - b^ (x_1 x_4,x_2,x_3) }[/math]
and r3.toCode() produces a version of the relation that can be used in Mathematica:
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] bp[x1 x3, x2, x4] bp[x1, x3, x4]
- bp[x1 x2, x3, x4] - bp[x1, x2, x4] - bp[x1 x4, x2, x3]
A few relations, such as r3, are already defined in syzygy.asy but more should be added.
Applying
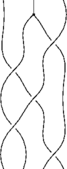
Now that we have relations, we can apply them to bigger braids. Let's start with the braid in the [math]\displaystyle{ \Phi }[/math] around B syzygy:
import syzygy; Braid b; b.n=4; b.add(bp,2); b.add(bp,0); b.add(bp,1); b.add(bp,0); b.add(bp,2); b.add(phi,1);
After skipping the lowest knot, we can apply R3 to the next three knots:
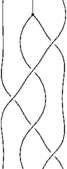
Braid bb=apply(r3, b, 1, 0);
here apply(r, b, k, n) means we are applying the relation r to the braid b at the place in the braid found by counting k components up from the bottom component and n strands in from the leftmost strand. apply does not modify the original braid, but returns the result of applying the relation (stored here as bb):
This went from the left hand side of the relation to the right hand side. To apply a relation in reverse, simply prefix it by a minus sign. For example apply(-r3, bb, 1, 0) will yield a braid equivalent to our original. When applying a relation, the script first checks that the one side of the relation matches that portion of the braid, and will give a (somewhat cryptic) error if the relation cannot be applied.
In our braids, the components are placed from bottom to top in a fixed order. Sometimes when building syzygies, it is neccessary to swap the order that these components occur. This is done by the swap method. For instance, starting from b, we can swap the two bottom crossings:
Braid swapped=b.swap(0,1);
Remember that components are ordered from bottom to top, starting at 0. Again, the script checks to make sure the swap is valid (ie. changing the order of the two components, doesn't actually change the knot) and will issue an error if it isn't.
Syzygies
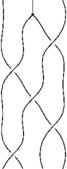
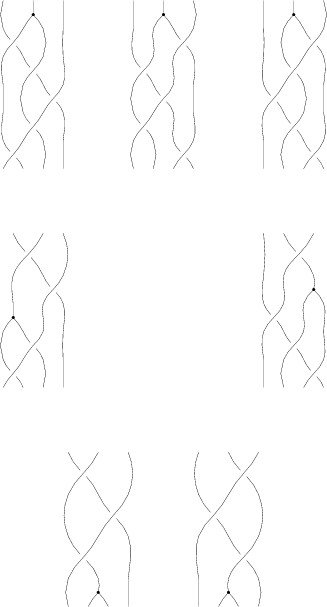
One could manually apply relations and swaps, and make a whole bunch of braids, but it would be annoying to keep track of them all. Thankfully, the Syzygy structure does that for us. For example, here is the complete code for the [math]\displaystyle{ \Phi }[/math] around B syzygy:
import syzygy; // Phi around B Braid initial; initial.n=4; initial.add(bp,2); initial.add(bp,0); initial.add(bp,1); initial.add(bp,0); initial.add(bp,2); initial.add(phi,1); Syzygy pb; pb.lsym="\Phi B"; pb.codename="PhiAroundB"; pb.initial=initial; pb.apply(r3,1,0); pb.apply(r4a,3,1); pb.swap(2,3); pb.apply(r4b,0,1); pb.apply(-r3,1,0); pb.apply(-r4a,0,0); pb.swap(2,3); pb.apply(-r4b,3,0); pb.apply(r3,1,1); pb.draw();
and the result
Again, like relations, we can use pb.toLinear()
| [math]\displaystyle{ \Phi B(x_1,x_2,x_3,x_4,x_5) = }[/math] | [math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_5) \rho_{4a}(x_1 x_5,x_2,x_3,x_4) \rho_{4b}(x_1 x_2,x_3,x_4,x_5) }[/math] |
| [math]\displaystyle{ - \rho_3(x_1,x_2,x_3 x_4,x_5) - \rho_{4a}(x_1,x_2,x_3,x_4) }[/math] | |
| [math]\displaystyle{ - \rho_{4b}(x_1,x_3,x_4,x_5) \rho_3(x_1 x_3,x_2,x_4,x_5). }[/math] |
and pb.toCode()
PhiAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] rho4a[x1 x5, x2, x3, x4] rho4b[x1 x2, x3, x4, x5] - rho3[x1, x2, x3 x4, x5] - rho4a[x1, x2, x3, x4] - rho4b[x1, x3, x4, x5] rho3[x1 x3, x2, x4, x5]
to give the formulas for the syzygies.
The Syzygy structure assumes that after the last application of a relation, the braid is in the same form as the start, so it won't draw the last braid. This is annoying when building a syzygy, so it can be turned off by pb.cyclic=false; If you set bp.showall=true; the syzygy will draw all changes to the braid, including swaps. Finally, setting bp.number=true; will print numbers on the diagrams so you can follow them around.
Conclusion
Example syzygyies and the latest version of the script can be found in the syzygy directory on the course Subversion repository [1]. Please contact me if you have any questions or suggestions. Good luck and happy syzyging!