09-240:HW7: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{09-240/Navigation}} |
{{09-240/Navigation}} |
||
{{In Preparation}} |
|||
* '''Read''' sections 2.4, 3.1 and 3.2 in our textbook. Remember that reading math isn't like reading a novel! If you read a novel and miss a few details most likely you'll still understand the novel. But if you miss a few details in a math text, often you'll miss everything that follows. So reading math takes reading and rereading and rerereading and a lot of thought about what you've read. Also, '''preread''' section 2.5, just to get a feel for the future. |
|||
* '''Solve''' problems 1, 2, <u>3a</u>, and 3b on pages 96-97, problems 1, 2, 4 and <u>9</u> on pages 106-107, problems 1, 2, and 9 on pages 151-152, and problems 1, 2aceg, <u>2bdf</u>, 7, <u>19</u>, and 21 on pages 165-168 but submit only your solutions of the underlined problems. |
|||
This assignment is due at the tutorials on Thursday November 19. |
|||
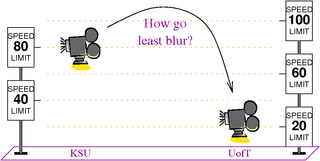
'''Just For Fun.''' Assume the Earth is flat. We want to fly a virtual video camera from a mile above the Kansas State University campus (so that the whole thing is in sight) to a kilometer above the University of Toronto campus (so that the whole thing is in sight) in 10 seconds or less, so that the resulting movie will have the least blur. Clearly, we shouldn't fly at a constant elevation, for a camera moving so fast so close to the ground will suffer immense motion blur. Instead, we should fly up and thus zoom out, then move sideways fast but while we're far, and then zoom back in again. But what's the precise optimal path? And what should our speed be at any point along that path? |
|||
[[Image:KSU2UofT.png|center|320px]] |
|||
Latest revision as of 11:52, 11 November 2009
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- Read sections 2.4, 3.1 and 3.2 in our textbook. Remember that reading math isn't like reading a novel! If you read a novel and miss a few details most likely you'll still understand the novel. But if you miss a few details in a math text, often you'll miss everything that follows. So reading math takes reading and rereading and rerereading and a lot of thought about what you've read. Also, preread section 2.5, just to get a feel for the future.
- Solve problems 1, 2, 3a, and 3b on pages 96-97, problems 1, 2, 4 and 9 on pages 106-107, problems 1, 2, and 9 on pages 151-152, and problems 1, 2aceg, 2bdf, 7, 19, and 21 on pages 165-168 but submit only your solutions of the underlined problems.
This assignment is due at the tutorials on Thursday November 19.
Just For Fun. Assume the Earth is flat. We want to fly a virtual video camera from a mile above the Kansas State University campus (so that the whole thing is in sight) to a kilometer above the University of Toronto campus (so that the whole thing is in sight) in 10 seconds or less, so that the resulting movie will have the least blur. Clearly, we shouldn't fly at a constant elevation, for a camera moving so fast so close to the ground will suffer immense motion blur. Instead, we should fly up and thus zoom out, then move sideways fast but while we're far, and then zoom back in again. But what's the precise optimal path? And what should our speed be at any point along that path?