06-1350/Class Notes for Thursday November 16: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
* <math>{\mathcal A}(\uparrow_n)</math> is a VS-algebra (see more at [[VS, TS and TG Algebras]]). |
* <math>{\mathcal A}(\uparrow_n)</math> is a VS-algebra (see more at [[VS, TS and TG Algebras]]). |
||
* In the coordinates above, write the <math>TR\Phi B</math> relations in various algebraic notations. |
* In the coordinates above, write the <math>TR\Phi B</math> relations in various algebraic notations. |
||
** R4: <math>(1230)^\star B |
** R4: <math>(1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star\Phi=(1123)^\star\Phi\cdot(1233)^\star B</math> or <math>(B_{1a}B_{2a}\Phi_{1a}; B_{1b}B_{2b}; B_{1c}B_{2a}\Phi_{1b}; B_{2c}\Phi_{1c}) = (\Phi_{2a}B_{3a}; \Phi_{2a}B_{3b}; \Phi_{2b}B_{3c}; \Phi_{2c}B_{3c})</math>. |
||
** R3: <math>(1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star B = (1123)^\star B\cdot(1203)^\star B\cdot(1231)^\star B</math> or <math>(B_{1a}B_{2a}B_{3a}; B_{1b}B_{2b}; B_{1c}B_{2a}B_{3b}; B_{2c}B_{3c}) = (B_{4a}B_{5a}B_{6a}; B_{4a}B_{5b}B_{6b}; B_{4b}B_{6c}; B_{4c}B_{5c}B_{6a})</math>. |
|||
| ⚫ | |||
** <math>B^{\pm}</math> in terms of <math>\Phi</math> and <math>R</math> and <math>R</math> in terms of <math>T</math>. |
** <math>B^{\pm}</math> in terms of <math>\Phi</math> and <math>R</math> and <math>R</math> in terms of <math>T</math>. |
||
| ⚫ | |||
** Symmetry of <math>\Phi</math> and of <math>B^{\pm}</math>. |
** Symmetry of <math>\Phi</math> and of <math>B^{\pm}</math>. |
||
** <math>u</math>, <math>d</math> and <math>\#</math> |
** <math>u</math>, <math>d</math> and <math>\#</math> |
||
Revision as of 21:36, 15 November 2006
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
In Preparation
The information below is preliminary and cannot be trusted! (v)
Today's Agenda
- Sweeping clean a tree and [math]\displaystyle{ {\mathcal A}(\Gamma)\equiv{\mathcal A}(\uparrow_{b_1(\Gamma)}) }[/math].
- [math]\displaystyle{ {\mathcal A}(\uparrow_n) }[/math] is a VS-algebra (see more at VS, TS and TG Algebras).
- In the coordinates above, write the [math]\displaystyle{ TR\Phi B }[/math] relations in various algebraic notations.
- R4: [math]\displaystyle{ (1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star\Phi=(1123)^\star\Phi\cdot(1233)^\star B }[/math] or [math]\displaystyle{ (B_{1a}B_{2a}\Phi_{1a}; B_{1b}B_{2b}; B_{1c}B_{2a}\Phi_{1b}; B_{2c}\Phi_{1c}) = (\Phi_{2a}B_{3a}; \Phi_{2a}B_{3b}; \Phi_{2b}B_{3c}; \Phi_{2c}B_{3c}) }[/math].
- R3: [math]\displaystyle{ (1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star B = (1123)^\star B\cdot(1203)^\star B\cdot(1231)^\star B }[/math] or [math]\displaystyle{ (B_{1a}B_{2a}B_{3a}; B_{1b}B_{2b}; B_{1c}B_{2a}B_{3b}; B_{2c}B_{3c}) = (B_{4a}B_{5a}B_{6a}; B_{4a}B_{5b}B_{6b}; B_{4b}B_{6c}; B_{4c}B_{5c}B_{6a}) }[/math].
- R2, R1
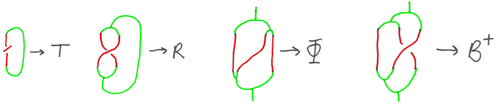
- [math]\displaystyle{ B^{\pm} }[/math] in terms of [math]\displaystyle{ \Phi }[/math] and [math]\displaystyle{ R }[/math] and [math]\displaystyle{ R }[/math] in terms of [math]\displaystyle{ T }[/math].
- Symmetry of [math]\displaystyle{ \Phi }[/math] and of [math]\displaystyle{ B^{\pm} }[/math].
- [math]\displaystyle{ u }[/math], [math]\displaystyle{ d }[/math] and [math]\displaystyle{ \# }[/math]
- Idempotence for [math]\displaystyle{ T }[/math], [math]\displaystyle{ R }[/math], [math]\displaystyle{ \Phi }[/math] and [math]\displaystyle{ B^{\pm} }[/math].