06-1350/Class Notes for Thursday November 16: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{06-1350/Navigation}} |
{{06-1350/Navigation}} |
||
{{In Preparation}} |
|||
==Today's Agenda== |
==Today's Agenda== |
||
===Formulas are a Chore (Bore?)=== |
|||
* Sweeping clean a tree and <math>{\mathcal A}(\Gamma)\equiv{\mathcal A}(\uparrow_{b_1(\Gamma)})</math>. |
* Sweeping clean a tree and <math>{\mathcal A}(\Gamma)\equiv{\mathcal A}(\uparrow_{b_1(\Gamma)})</math>. |
||
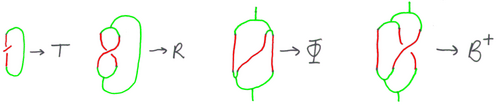
[[Image:06-1350-TRPhiB.png|center|500px]] |
[[Image:06-1350-TRPhiB.png|center|500px]] |
||
* <math>{\mathcal A}(\uparrow_n)</math> is a VS-algebra (see more at [[VS, TS and TG Algebras]]). |
* <math>{\mathcal A}(\uparrow_n)</math> is a VS-algebra (see more at [[VS, TS and TG Algebras]]). |
||
* In the coordinates above, write the <math>TR\Phi B</math> relations in various algebraic notations. |
* In the coordinates above, write the <math>TR\Phi B</math> relations in various algebraic notations. |
||
** R4: <math>(1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star\Phi=(1123)^\star\Phi\cdot(1233)^\star B</math> or <math>(B_{1a}B_{2a}\Phi_{1a}; B_{1b}B_{2b}; B_{1c}B_{2a}\Phi_{1b}; B_{2c}\Phi_{1c}) = (\Phi_{2a}B_{3a}; \Phi_{2a}B_{3b}; \Phi_{2b}B_{3c}; \Phi_{2c}B_{3c})</math>. |
** R4: <math>(1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star\Phi=(1123)^\star\Phi\cdot(1233)^\star B</math> or <math>(B_{1a}B_{2a}\Phi_{1a}; B_{1b}B_{2b}; B_{1c}B_{2a}\Phi_{1b}; B_{2c}\Phi_{1c}) = (\Phi_{2a}B_{3a}; \Phi_{2a}B_{3b}; \Phi_{2b}B_{3c}; \Phi_{2c}B_{3c})</math>. |
||
| Line 13: | Line 15: | ||
** R2: <math>(123)^\star B^\pm\cdot(132)^\star B^\mp=1_3</math> or <math>(B^\pm_{1a}B^\mp_{2a}; B^\pm_{2b}B^\mp_{3c}; B^\pm_{1c}B^\mp_{2b}) = (1;1;1)</math>. |
** R2: <math>(123)^\star B^\pm\cdot(132)^\star B^\mp=1_3</math> or <math>(B^\pm_{1a}B^\mp_{2a}; B^\pm_{2b}B^\mp_{3c}; B^\pm_{1c}B^\mp_{2b}) = (1;1;1)</math>. |
||
** R1: <math>(B^\pm_a; B^\pm_bB^\pm_c)=(1;T^{\pm 2})</math>. |
** R1: <math>(B^\pm_a; B^\pm_bB^\pm_c)=(1;T^{\pm 2})</math>. |
||
* But for now, skip the writing of the following relations: |
|||
** Symmetry of <math>\Phi</math> and of <math>B^{\pm}</math>. |
** Symmetry of <math>\Phi</math> and of <math>B^{\pm}</math>. |
||
** <math>u</math>, <math>d</math> and <math>\#</math> |
** <math>u</math>, <math>d</math> and <math>\#</math> |
||
| Line 18: | Line 21: | ||
** <math>B^{\pm}</math> in terms of <math>\Phi</math> and <math>R</math> and <math>R</math> in terms of <math>T</math>. |
** <math>B^{\pm}</math> in terms of <math>\Phi</math> and <math>R</math> and <math>R</math> in terms of <math>T</math>. |
||
===Exponentiation is a Miracle=== |
|||
'''General Principle.''' Believe not, until you see a running program. |
|||
* Description of the problem. |
|||
* Beads and strands. |
|||
* The perturbative approach, linearization. |
|||
* The syzygies: relations between the errors. |
|||
* The Hochschild complex and homology. |
|||
Latest revision as of 09:29, 16 November 2006
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Today's Agenda
Formulas are a Chore (Bore?)
- Sweeping clean a tree and .
- is a VS-algebra (see more at VS, TS and TG Algebras).
- In the coordinates above, write the relations in various algebraic notations.
- R4: or .
- R3: or .
- R2: or .
- R1: .
- But for now, skip the writing of the following relations:
- Symmetry of and of .
- , and
- Idempotence for , , and .
- in terms of and and in terms of .
Exponentiation is a Miracle
- Description of the problem.
- Beads and strands.
- The perturbative approach, linearization.
- The syzygies: relations between the errors.
- The Hochschild complex and homology.