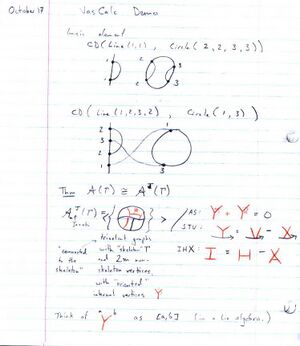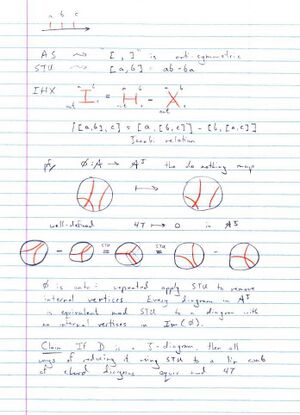06-1350/Class Notes for Tuesday October 17: Difference between revisions
No edit summary |
(Added scanned class notes.) |
||
| Line 27: | Line 27: | ||
{{note|Drinfeld_91}} V. G. Drinfel'd, ''On quasitriangular Quasi-Hopf algebras and a group closely connected with <math>\operatorname{Gal}(\bar{\mathbb Q}/{\mathbb Q})</math>,'' Leningrad Math. J. '''2''' (1991) 829-860. |
{{note|Drinfeld_91}} V. G. Drinfel'd, ''On quasitriangular Quasi-Hopf algebras and a group closely connected with <math>\operatorname{Gal}(\bar{\mathbb Q}/{\mathbb Q})</math>,'' Leningrad Math. J. '''2''' (1991) 829-860. |
||
==Scanned Notes== |
|||
{| align=left |
|||
|[[Image:06-1350-scan1017-0001.jpg|thumb]] |
|||
|[[Image:06-1350-scan1017-0002.jpg|thumb]] |
|||
|} |
|||
Latest revision as of 15:26, 24 October 2006
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
VasCalc Demo
See Siddarth Sankaran first demo of his and Zavosh Amir-Khosravi's VasCalc project: VasCalcDemo1.nb.
Analysis in Algebra
Question. What is the simplest theorem you know in algebra, whose proof requires, really requires, analysis?
Comment 1. It definitely isn't "The Fundamental Theorem of Algebra", which says that the field is algebraically closed. Despite its name, this theorem is not at all a theorem in algebra - its formulation requires the complex numbers, and these are analytic entities to start with.
Comment 2. So what's algebra? The integers, their quotients (aka the rationals), polynomial rings, their quotients, and in general, anything discrete. And what's analysis? Anything that involves taking limits (or really, least upper bounds). In particular, integration and the non-symbolic solution of differential equation.
Comment 3. Many theorems in analytic number theory "don't count" for the purpose of my question. Either their formulations are not-really-algebraic, or their proofs involves inequalities (say) between integrals that can be re-derived using sufficiently fine discrete approximations.
Comment 4. Later in class we will see the best answer I know for the above question. We will see an algebraic equation, defined over the rationals and whose solutions are rational. Yet the only proofs I know that a solution exists involves writing some hairy integrals (and evaluating them exactly, not just approximately), or solving a certain differential equation that does not have a closed-form symbolic solution.
To me this is a stain that needs to be removed from our otherwise elegant theory. I can't believe it really is necessary to use the reals, so I do believe there must be a way around it. But as I don't know the way, I know I'm missing something big.
The theorem in question is the existence of "rational horizontal Drinfel'd associators" proven by Drinfel'd in [Drinfeld_90] and [Drinfeld_91]. It is closely related to the existence of universal finite type invariants for knotted trivalent graphs.
Comment 5. Perhaps the bothersome fact about the existence of rational horizontal Drinfel'd associators can be stated in a different manner: It is a theorem saying that certain algebraic equalities over the rationals have rational solutions, yet its proof genuinely involves inequalities. Do you know other examples?
References.
[Drinfeld_90] ^ V. G. Drinfel'd, Quasi-Hopf algebras, Leningrad Math. J. 1 (1990) 1419-1457.
[Drinfeld_91] ^ V. G. Drinfel'd, On quasitriangular Quasi-Hopf algebras and a group closely connected with , Leningrad Math. J. 2 (1991) 829-860.