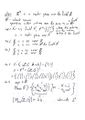12-240/Classnotes for Tuesday September 25: Difference between revisions
From Drorbn
Jump to navigationJump to search
| Line 12: | Line 12: | ||
Then, (+): VxV->V is (v,w)= v+w; (.): FxV->V is (c,v)=cv |
Then, (+): VxV->V is (v,w)= v+w; (.): FxV->V is (c,v)=cv |
||
Such that |
|||
VS1 <math>\forall\!\,</math> x, y <math>\in\!\,</math> V: x+y = y+x |
|||
VS2 |
|||
VS3 |
|||
VS4 |
|||
VS5 |
|||
VS6 |
|||
==Scanned Notes by [[User:Richardm|Richardm]]== |
==Scanned Notes by [[User:Richardm|Richardm]]== |
||
Revision as of 18:34, 25 September 2012
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Today's class dealt with the properties of vector spaces.
Definition
Let F is a field, a vector space V over F is a set V of vectors with special element O ( of V) and tow operations: (+): VxV->V, (.): FxV->V
VxV={(v,w): v,w V}
FxV={(c,v): c F, v V}
Then, (+): VxV->V is (v,w)= v+w; (.): FxV->V is (c,v)=cv
Such that
VS1 x, y V: x+y = y+x
VS2 VS3 VS4 VS5 VS6