10-327: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
===Text=== |
===Text=== |
||
James Munkres' [http://vig.pearsoned.ca/catalog/academic/product/0,4096,0131816292,00.html Topology] (see [[10-327/Errata to Munkres' Book|Errata]]). The topology texts by Dugundji and Massey are also recommended, and many other texts are also available. (A useful principle to know is that many math texts are available online. Web search for |
James Munkres' [http://vig.pearsoned.ca/catalog/academic/product/0,4096,0131816292,00.html Topology] (see [[10-327/Errata to Munkres' Book|Errata]]). The topology texts by Dugundji and Massey are also recommended, and many other texts are also available. (A useful principle to know is that many math texts are available online. Web search for name of text + name of author + pdf or djvu). |
||
===Further Resources=== |
===Further Resources=== |
||
| Line 19: | Line 19: | ||
* [[10-327/Errata to Munkres' Book|Errata to Munkres' Book]]. |
* [[10-327/Errata to Munkres' Book|Errata to Munkres' Book]]. |
||
===Current Interest=== |
|||
| ⚫ | |||
[[Image:10-327-CompactnessInMetricSpaces.png|center|480px]] |
|||
===Previous Topic=== |
|||
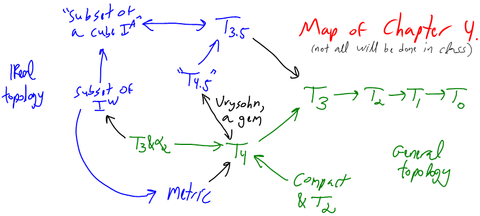
[[Image:10-327-MapOfChapter4.png|center|480px]] |
|||
| ⚫ | |||
Hello all. Just a couple points of possible interest for your problem sets. First, they do not need to be extremely detailed or lengthy, however please make sure that you do mention that an argument comes from a theorem or lemma (unless it is very obvious). You can be very concise as long as you reference your arguments like this. A good length you should aim for is 4 pages hand written. It is also a very good exercise to look over a question you have written out and ask yourself what the main arguments you used were. How can I summarize this argument? |
Hello all. Just a couple points of possible interest for your problem sets. First, they do not need to be extremely detailed or lengthy, however please make sure that you do mention that an argument comes from a theorem or lemma (unless it is very obvious). You can be very concise as long as you reference your arguments like this. A good length you should aim for is 4 pages hand written. It is also a very good exercise to look over a question you have written out and ask yourself what the main arguments you used were. How can I summarize this argument? |
||
Latest revision as of 18:57, 19 December 2010
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Introduction to Topology
Department of Mathematics, University of Toronto, Fall 2010
Agenda: Understand "continuity" in the most abstract, learn about "the fundamental groups" and maybe touch "surfaces".
Instructor: Dror Bar-Natan, drorbn@math.toronto.edu (Wiki before Email!), Bahen 6178, 416-946-5438. Office hours: by appointment.
Classes: Mondays 2-3 and Thursdays 2-4 in Sydney Smith 1070.
| Teaching Assistant: David Reiss, david.reiss@utoronto.ca, SS 622. |
Text
James Munkres' Topology (see Errata). The topology texts by Dugundji and Massey are also recommended, and many other texts are also available. (A useful principle to know is that many math texts are available online. Web search for name of text + name of author + pdf or djvu).
Further Resources
- Undergraduate Information at the UofT Math Department
- Undergraduate Course Descriptions.
- My 10-327 notebook.
- My 2005-06 Math 1300/427 web site.
- My 2004-05 Math 1300/427 web site.
- Errata to Munkres' Book.
Current Interest
Previous Topic
A note from the TA
Hello all. Just a couple points of possible interest for your problem sets. First, they do not need to be extremely detailed or lengthy, however please make sure that you do mention that an argument comes from a theorem or lemma (unless it is very obvious). You can be very concise as long as you reference your arguments like this. A good length you should aim for is 4 pages hand written. It is also a very good exercise to look over a question you have written out and ask yourself what the main arguments you used were. How can I summarize this argument?
I noticed many students have confused the topology with the basis. The basis generates the topology. For example, not all sets in the product topology of XxY are of the form UxV where U is open in X and V is open in Y. (Consider (0,1)x(0,1) union (2,3)x(2,3) <--- open since it is the union of open sets, yet it cannot be expressed as UxV. Draw a picture if this is unclear).
Cheers