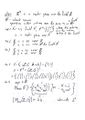12-240/Classnotes for Tuesday September 25: Difference between revisions
| (One intermediate revision by the same user not shown) | |||
| Line 58: | Line 58: | ||
1. Cancellation Laws |
1. Cancellation Laws |
||
(a) x+z=y+z ==> x=y |
(a) x+z=y+z ==> x=y |
||
(b) ax |
(b) ax=ay,a≠0 ==> x=y |
||
(c) x≠0 of V, ax=bx ==> a=b |
(c) x≠0 of V, ax=bx ==> a=b |
||
| Line 67: | Line 67: | ||
4.(0 of F)x = 0 of V |
4.(0 of F)x = 0 of V |
||
5. |
5. a∙0=0 |
||
6. (-a)x= - |
6. (-a)x = -(ax) = a(-x) |
||
7. |
7. a∙v=0 <==> a=0 or v=0 |
||
==Proof== |
==Proof== |
||
Latest revision as of 04:41, 7 December 2012
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Today's class dealt with the properties of vector spaces.
Definition
Let F be a field. A vector space V over F is a set V of vectors with special element O ( of V) and two operations: (+): VxV->V, (.): FxV->V
VxV={(v,w): v,w [math]\displaystyle{ \in\!\, }[/math] V}
FxV={(c,v): c [math]\displaystyle{ \in\!\, }[/math] F, v [math]\displaystyle{ \in\!\, }[/math] V}
Then, (+): VxV->V is (v,w)= v+w; (.): FxV->V is (c,v)=cv
Such that
VS1 [math]\displaystyle{ \forall\!\, }[/math] x, y [math]\displaystyle{ \in\!\, }[/math] V: x+y = y+x
VS2 [math]\displaystyle{ \forall\!\, }[/math] x, y, z [math]\displaystyle{ \in\!\, }[/math] V: x+(y+z) = (x+y)+z
VS3 [math]\displaystyle{ \forall\!\, }[/math] x [math]\displaystyle{ \in\!\, }[/math] V: 0 ( of V) +x = x
VS4 [math]\displaystyle{ \forall\!\, }[/math] x [math]\displaystyle{ \in\!\, }[/math] V, [math]\displaystyle{ \exists \!\, }[/math] V [math]\displaystyle{ \in\!\, }[/math] V: v + x= 0 ( of V)
VS5 [math]\displaystyle{ \forall\!\, }[/math] x [math]\displaystyle{ \in\!\, }[/math] V, 1 (of F) .x = x
VS6 [math]\displaystyle{ \forall\!\, }[/math] a, b [math]\displaystyle{ \in\!\, }[/math] F, [math]\displaystyle{ \forall\!\, }[/math] x [math]\displaystyle{ \in\!\, }[/math] V: (ab)x = a(bx)
VS7 [math]\displaystyle{ \forall\!\, }[/math] a [math]\displaystyle{ \in\!\, }[/math] F, [math]\displaystyle{ \forall\!\, }[/math] x, y [math]\displaystyle{ \in\!\, }[/math] V: a(x + y)= ax + ay
VS8 [math]\displaystyle{ \forall\!\, }[/math] a, b [math]\displaystyle{ \in\!\, }[/math] F, [math]\displaystyle{ \forall\!\, }[/math] x [math]\displaystyle{ \in\!\, }[/math] V: (a + b)x = ax + bx
Examples
Properties
Polynomials
Definition : Pn(F) = {all polynomials of degree less than or equal to n with coefficients in F}
= {anx^n + an-1x^n-1 + ... + a1x^1 + a1x^1}
0 = 0x^n + 0x^n-1 +...+ 0x^0
addition and multiplication: as you imagine
P(f) = {all polynomials with coefficients in F}
Take F= Z/2 |F| = 2
|P(F)| = infinite
in Pn(Z/2) x^3≠x^2
x^3 = 1*x^3+0x^2+0x+O = f
x^2 = 1*x^2+0x+0 = g
yet f(0)= g(0) and f(1)=g(1)
Theorem
1. Cancellation Laws
(a) x+z=y+z ==> x=y (b) ax=ay,a≠0 ==> x=y (c) x≠0 of V, ax=bx ==> a=b
2. 0 of V is unique
3. Negatives are unique (so subtraction makes sense
4.(0 of F)x = 0 of V
5. a∙0=0
6. (-a)x = -(ax) = a(-x)
7. a∙v=0 <==> a=0 or v=0
Proof
1. (a) x+z=y+z
Find a w s.t. z+w=0 (V.S. 4)
(x+z)+w = (y+z)+w
Use VS2
x+(z+w) = y +(z+w)
x + 0 = y + o
Use VS3 x=y