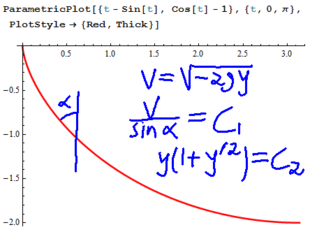12-267/Homework Assignment 3: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 13: | Line 13: | ||
# <math>y\mapsto\int_a^b\frac{y'^2}{x^3}dx</math>. |
# <math>y\mapsto\int_a^b\frac{y'^2}{x^3}dx</math>. |
||
# <math>y\mapsto\int_a^b(y^2+y'^2+2ye^x)dx</math>. |
# <math>y\mapsto\int_a^b(y^2+y'^2+2ye^x)dx</math>. |
||
# <span style="color: red">Postponed!</span> <math>y\mapsto\int_0^1(y'^2+x^2)dx</math> subject to <math>\int_0^1y^2dx=2</math> and <math>y(0)=0</math> and <math>y(1)= |
# <span style="color: red">Postponed!</span> <math>y\mapsto\int_0^1(y'^2+x^2)dx</math> subject to <math>\int_0^1y^2dx=2</math> and <math>y(0)=0</math> and <math>y(1)=0</math>. |
||
'''Task 3.''' A roach <math>R</math> I once met was mortally afraid of walls, and so when it walked on my kitchen's floor, its speed was exactly proportional to its distance from the nearest wall (that is, very near a wall it crawled very slowly, while in the centre of the room it run around quickly and happily). As a step towards simplifying <math>R</math>'s life, help it find the fastest path from one point in the upper half plane <math>\{y>0\}</math> to another point in the upper half plane, assuming there is only one wall around, built along the <math>x</math>-axis <math>y=0</math>. |
'''Task 3.''' A roach <math>R</math> I once met was mortally afraid of walls, and so when it walked on my kitchen's floor, its speed was exactly proportional to its distance from the nearest wall (that is, very near a wall it crawled very slowly, while in the centre of the room it run around quickly and happily). As a step towards simplifying <math>R</math>'s life, help it find the fastest path from one point in the upper half plane <math>\{y>0\}</math> to another point in the upper half plane, assuming there is only one wall around, built along the <math>x</math>-axis <math>y=0</math>. |
||
{{Template:12-267:Dror/Students Divider}} |
|||
'''Solution to Task 1.''' --[[User:Twine|Twine]] 18:11, 24 October 2012 (EDT) |
|||
Let <math>\sum_{n=1}^\infty c_n = S</math>. We have that <math>\lim_{n \rightarrow \infty} c_n = 0</math>. |
|||
Let <math>\epsilon > 0</math>. |
|||
<math>\exists N \in \mathbb{Z}^+</math> such that <math>\sum_{n=1}^N c_n > S - \epsilon</math>. |
|||
Choose such an N. Then <math>\sum_{n=N}^{\infty} c_n < \epsilon</math>. |
|||
Then <math>\forall x \in X, \forall m > N, n>N</math>, we have <math>|\Phi_n(x) - \Phi_m(x)| < \epsilon</math>. |
|||
As this result is independent of our choice of x, we have by the cauchy criterion that <math>\Phi_n</math> is uniformly convergent and <math>\lim_{n \rightarrow \infty} \Phi_n(x) = \Phi(x)</math> exists. |
|||
Solutions to HW3: [[User:Mathstudent|Mathstudent]] |
|||
<gallery> |
|||
Image:012.jpg|page 1 |
|||
Image:013.jpg|page 2 |
|||
Image:014.jpg|page 3 |
|||
Image:015.jpg|page 4 |
|||
</gallery> |
|||
Latest revision as of 08:49, 25 October 2012
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due at the tutorial on Tuesday October 9. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.
Task 0. Identify yourself in the Class Photo!
Task 1. Let [math]\displaystyle{ \phi_n\colon X\to{\mathbb R} }[/math] be a sequence of functions defined on some set [math]\displaystyle{ X }[/math], and suppose that some sequence [math]\displaystyle{ c_n }[/math] of non-negative reals is given such that for every [math]\displaystyle{ x\in X }[/math], [math]\displaystyle{ |\phi_n(x)-\phi_{n+1}(x)|\leq c_n }[/math]. Suppose also that [math]\displaystyle{ \sum_{n=1}^\infty c_n }[/math] is finite. Prove that the sequence [math]\displaystyle{ \phi_n }[/math] is uniformly convergent.
Task 2. Find the extrema of the following functionals:
- [math]\displaystyle{ y\mapsto \int_0^1y'dx }[/math] subject to [math]\displaystyle{ y(0)=0 }[/math] and [math]\displaystyle{ y(1)=1 }[/math].
- [math]\displaystyle{ y\mapsto \int_0^1yy'dx }[/math] subject to [math]\displaystyle{ y(0)=0 }[/math] and [math]\displaystyle{ y(1)=1 }[/math].
- [math]\displaystyle{ y\mapsto \int_0^1xyy'dx }[/math] subject to [math]\displaystyle{ y(0)=0 }[/math] and [math]\displaystyle{ y(1)=1 }[/math].
- [math]\displaystyle{ y\mapsto\int_a^b\frac{y'^2}{x^3}dx }[/math].
- [math]\displaystyle{ y\mapsto\int_a^b(y^2+y'^2+2ye^x)dx }[/math].
- Postponed! [math]\displaystyle{ y\mapsto\int_0^1(y'^2+x^2)dx }[/math] subject to [math]\displaystyle{ \int_0^1y^2dx=2 }[/math] and [math]\displaystyle{ y(0)=0 }[/math] and [math]\displaystyle{ y(1)=0 }[/math].
Task 3. A roach [math]\displaystyle{ R }[/math] I once met was mortally afraid of walls, and so when it walked on my kitchen's floor, its speed was exactly proportional to its distance from the nearest wall (that is, very near a wall it crawled very slowly, while in the centre of the room it run around quickly and happily). As a step towards simplifying [math]\displaystyle{ R }[/math]'s life, help it find the fastest path from one point in the upper half plane [math]\displaystyle{ \{y\gt 0\} }[/math] to another point in the upper half plane, assuming there is only one wall around, built along the [math]\displaystyle{ x }[/math]-axis [math]\displaystyle{ y=0 }[/math].
| Dror's notes above / Student's notes below |
Solution to Task 1. --Twine 18:11, 24 October 2012 (EDT)
Let [math]\displaystyle{ \sum_{n=1}^\infty c_n = S }[/math]. We have that [math]\displaystyle{ \lim_{n \rightarrow \infty} c_n = 0 }[/math].
Let [math]\displaystyle{ \epsilon \gt 0 }[/math].
[math]\displaystyle{ \exists N \in \mathbb{Z}^+ }[/math] such that [math]\displaystyle{ \sum_{n=1}^N c_n \gt S - \epsilon }[/math].
Choose such an N. Then [math]\displaystyle{ \sum_{n=N}^{\infty} c_n \lt \epsilon }[/math].
Then [math]\displaystyle{ \forall x \in X, \forall m \gt N, n\gt N }[/math], we have [math]\displaystyle{ |\Phi_n(x) - \Phi_m(x)| \lt \epsilon }[/math].
As this result is independent of our choice of x, we have by the cauchy criterion that [math]\displaystyle{ \Phi_n }[/math] is uniformly convergent and [math]\displaystyle{ \lim_{n \rightarrow \infty} \Phi_n(x) = \Phi(x) }[/math] exists.
Solutions to HW3: Mathstudent