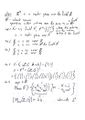12-240/Classnotes for Tuesday September 25: Difference between revisions
No edit summary |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 5: | Line 5: | ||
== Definition == |
== Definition == |
||
Let F |
Let F be a field. A vector space V over F is a set V of vectors with special element O ( of V) and two operations: (+): VxV->V, (.): FxV->V |
||
VxV={(v,w): v,w <math>\in\!\,</math> V} |
VxV={(v,w): v,w <math>\in\!\,</math> V} |
||
| Line 30: | Line 30: | ||
VS8 <math>\forall\!\,</math> a, b <math>\in\!\,</math> F, <math>\forall\!\,</math> x <math>\in\!\,</math> V: (a + b)x = ax + bx |
VS8 <math>\forall\!\,</math> a, b <math>\in\!\,</math> F, <math>\forall\!\,</math> x <math>\in\!\,</math> V: (a + b)x = ax + bx |
||
== Examples == |
== Examples == |
||
| Line 37: | Line 36: | ||
==Properties == |
==Properties == |
||
==Polynomials== |
|||
'''Definition''' : Pn(F) = {all polynomials of degree less than or equal to n with coefficients in F} |
|||
= {anx^n + an-1x^n-1 + ... + a1x^1 + a1x^1} |
|||
0 = 0x^n + 0x^n-1 +...+ 0x^0 |
|||
addition and multiplication: as you imagine |
|||
P(f) = {all polynomials with coefficients in F} |
|||
Take F= '''Z'''/2 |F| = 2 |
|||
|P(F)| = infinite |
|||
in Pn('''Z'''/2) x^3≠x^2 |
|||
x^3 = 1*x^3+0x^2+0x+O = f |
|||
x^2 = 1*x^2+0x+0 = g |
|||
yet f(0)= g(0) and f(1)=g(1) |
|||
==Theorem== |
|||
1. Cancellation Laws |
|||
(a) x+z=y+z ==> x=y |
|||
(b) ax=ay,a≠0 ==> x=y |
|||
(c) x≠0 of V, ax=bx ==> a=b |
|||
2. 0 of V is unique |
|||
3. Negatives are unique (so subtraction makes sense |
|||
4.(0 of F)x = 0 of V |
|||
5. a∙0=0 |
|||
6. (-a)x = -(ax) = a(-x) |
|||
7. a∙v=0 <==> a=0 or v=0 |
|||
==Proof== |
|||
1. (a) x+z=y+z |
|||
Find a w s.t. z+w=0 (V.S. 4) |
|||
(x+z)+w = (y+z)+w |
|||
Use VS2 |
|||
x+(z+w) = y +(z+w) |
|||
x + 0 = y + o |
|||
Use VS3 x=y |
|||
==Scanned Notes by [[User:Richardm|Richardm]]== |
==Scanned Notes by [[User:Richardm|Richardm]]== |
||
Latest revision as of 04:41, 7 December 2012
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Today's class dealt with the properties of vector spaces.
Definition
Let F be a field. A vector space V over F is a set V of vectors with special element O ( of V) and two operations: (+): VxV->V, (.): FxV->V
VxV={(v,w): v,w V}
FxV={(c,v): c F, v V}
Then, (+): VxV->V is (v,w)= v+w; (.): FxV->V is (c,v)=cv
Such that
VS1 x, y V: x+y = y+x
VS2 x, y, z V: x+(y+z) = (x+y)+z
VS3 x V: 0 ( of V) +x = x
VS4 x V, V V: v + x= 0 ( of V)
VS5 x V, 1 (of F) .x = x
VS6 a, b F, x V: (ab)x = a(bx)
VS7 a F, x, y V: a(x + y)= ax + ay
VS8 a, b F, x V: (a + b)x = ax + bx
Examples
Properties
Polynomials
Definition : Pn(F) = {all polynomials of degree less than or equal to n with coefficients in F}
= {anx^n + an-1x^n-1 + ... + a1x^1 + a1x^1}
0 = 0x^n + 0x^n-1 +...+ 0x^0
addition and multiplication: as you imagine
P(f) = {all polynomials with coefficients in F}
Take F= Z/2 |F| = 2
|P(F)| = infinite
in Pn(Z/2) x^3≠x^2
x^3 = 1*x^3+0x^2+0x+O = f
x^2 = 1*x^2+0x+0 = g
yet f(0)= g(0) and f(1)=g(1)
Theorem
1. Cancellation Laws
(a) x+z=y+z ==> x=y (b) ax=ay,a≠0 ==> x=y (c) x≠0 of V, ax=bx ==> a=b
2. 0 of V is unique
3. Negatives are unique (so subtraction makes sense
4.(0 of F)x = 0 of V
5. a∙0=0
6. (-a)x = -(ax) = a(-x)
7. a∙v=0 <==> a=0 or v=0
Proof
1. (a) x+z=y+z
Find a w s.t. z+w=0 (V.S. 4)
(x+z)+w = (y+z)+w
Use VS2
x+(z+w) = y +(z+w)
x + 0 = y + o
Use VS3 x=y