12-267/Homework Assignment 4: Difference between revisions
No edit summary |
No edit summary |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{12-267/Navigation}} |
{{12-267/Navigation}} |
||
{{In Preparation}} |
|||
This assignment is due at the tutorial on Tuesday October 16. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong. |
This assignment is due at the tutorial on Tuesday October 16. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong. |
||
| Line 6: | Line 5: | ||
'''Task 0.''' Identify yourself in the [[12-267/Class Photo|Class Photo]]! |
'''Task 0.''' Identify yourself in the [[12-267/Class Photo|Class Photo]]! |
||
'''Task 1.''' Find the general solution of the Euler-Lagrange equation corresponding to the functional <math>J(y)=\int_a^bf(x)\sqrt{1+y'^2}dx</math>, and investigate the special cases <math>f(x)=\sqrt{x}</math> and <math>f(x)=x</math>. |
|||
'''Task 1.''' |
|||
'''Task 2.''' Find the extrema the following functional <math>y\mapsto\int_0^1(y'^2+x^2)dx</math> subject to <math>\int_0^1y^2dx=2</math> and <math>y(0)=0</math> and <math>y(1)=0</math>. (An earlier version of this assignment had by mistake <math>y(1)=1</math>, which leads to much uglier numbers. If you already solved the problem with <math>y(1)=1</math>, you may submit either solution). |
|||
'''Task 3.''' Solve the "power line problem": Of all the curves <math>y</math> with <math>y(a)=A</math> and <math>y(b)=B</math> and with total arc-length <math>l</math>, find the one with the least potential energy <math>\int_a^by\sqrt{1+y'^2}dx</math>. |
|||
'''Task 4.''' Find a necessary condition for a function <math>y</math> satisfying <math>y(a)=A</math>, <math>y'(a)=A'</math>, <math>y(b)=B</math>, and <math>y'(b)=B'</math> to be an extremal of a functional of the form <math>y\mapsto\int_a^bF(x,y,y',y'')dx</math>. |
|||
'''Task 5.''' Find the curve <math>y</math> joining the points <math>(0,0)</math> and <math>(1,0)</math> and for which the integral <math>\int_0^1y''^2dx</math> is minimal, if <math>y'(0)=a</math> and <math>y'(1)=b</math>. |
|||
{{Template:12-267:Dror/Students Divider}} |
|||
'''Solution to Task 4.''' --[[User:Twine|Twine]] 17:54, 24 October 2012 (EDT) |
|||
Let <math>h(x)</math> be any function defined on <math>[a, b]</math> with <math>h'(a) = h(a) = h'(b) = h(b) = 0</math>. For y to be an extremal of the functional with the boundary constraints given, we must have that <math>\frac{d}{d\epsilon} J(y + \epsilon h) |_{\epsilon = 0} = 0</math> for any such <math>h(x)</math>. |
|||
<math>\frac{d}{d\epsilon} J(y + \epsilon h) |_{\epsilon = 0}</math> |
|||
<math>= \frac{d}{d\epsilon} \int_a^b F(x, y+\epsilon h, y'+\epsilon h', y'' +\epsilon h'')dx|_{\epsilon = 0}</math> |
|||
<math>= \int_a^b (F_1 \cdot 0 + F_2 \cdot h + F_3 \cdot h' + F_4 \cdot h'')dx|_{\epsilon = 0}</math> |
|||
<math>= \int_a^b (F_2 \cdot h - F_3' \cdot h - F_4' \cdot h')dx + F_3 \cdot h|_a^b + F_4\cdot h'|_a^b</math> |
|||
<math>= \int_a^b (F_2 \cdot h - F_3' \cdot h + F_4'' \cdot h)dx + F_4'\cdot h|_a^b</math> |
|||
<math>= \int_a^b (F_2 - F_3' + F_4'') \cdot h dx</math> |
|||
For this to be equivalent to 0 for any h defined above, we must have |
|||
<math>F_y - \frac{d}{dx}F_{y'} + \frac{d^2}{dx^2}F_{y''} = 0</math> |
|||
'''Solution to Task 5.''' --[[User:Twine|Twine]] 17:54, 24 October 2012 (EDT) |
|||
We use the result of 4. As in this case F is independent of x, y, and y', the equation reduces to |
|||
<math>\frac{d^2}{dx^2}2y'' = 0</math> |
|||
<math>y'''' = 0</math> |
|||
This has the solution <math>y = c_0 + c_1 x + c_2 x^2 + c_3 x^3</math>. We can use the constraint equations <math>y(0) = 0</math>, <math>y(1) = 0</math>, <math>y'(0) = a</math>, <math>y'(1) = b</math> to show that <math>y = (b+a)x^3 - (2a + b)x^2 + ax</math>. Hence, This is the only y for which the functional is extremal. |
|||
[http://imgur.com/a/j99mC#0 Solutions to task 1,2 and 3] [[User:Vsbdthrsh|Vsbdthrsh]] |
|||
Latest revision as of 02:46, 1 November 2012
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due at the tutorial on Tuesday October 16. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.
Task 0. Identify yourself in the Class Photo!
Task 1. Find the general solution of the Euler-Lagrange equation corresponding to the functional , and investigate the special cases and .
Task 2. Find the extrema the following functional subject to and and . (An earlier version of this assignment had by mistake , which leads to much uglier numbers. If you already solved the problem with , you may submit either solution).
Task 3. Solve the "power line problem": Of all the curves with and and with total arc-length , find the one with the least potential energy .
Task 4. Find a necessary condition for a function satisfying , , , and to be an extremal of a functional of the form .
Task 5. Find the curve joining the points and and for which the integral is minimal, if and .
| Dror's notes above / Student's notes below |
Solution to Task 4. --Twine 17:54, 24 October 2012 (EDT)
Let be any function defined on with . For y to be an extremal of the functional with the boundary constraints given, we must have that for any such .
For this to be equivalent to 0 for any h defined above, we must have
Solution to Task 5. --Twine 17:54, 24 October 2012 (EDT)
We use the result of 4. As in this case F is independent of x, y, and y', the equation reduces to
This has the solution . We can use the constraint equations , , , to show that . Hence, This is the only y for which the functional is extremal.



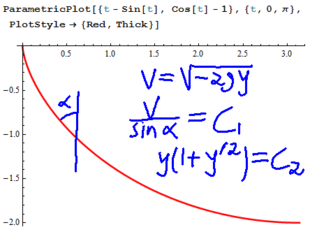






















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)












