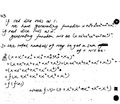| Welcome to Math 344!
|
| Edits to the Math 344 web sites no longer count for the purpose of good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 14
|
About This Class, Day One Handout, Tuesday, Hour 3 Handout, Thursday, Tutorial 1 Handout
|
| 2
|
Sep 21
|
Tuesday, Tutorial 2 Page 1, Tutorial 2 Page 2, Thursday, HW1
|
| 3
|
Sep 28
|
Tuesday, Class Photo, Tutorial 3 Page 1, Tutorial 3 Page 2, Thursday, HW2
|
| 4
|
Oct 5
|
Tuesday, Drawing  -cubes, Thursday, HW3 -cubes, Thursday, HW3
|
| 5
|
Oct 12
|
Tuesday, Tutorial Handout, Thursday, HW4
|
| 6
|
Oct 19
|
Tuesday, Tutorial Handout, Thursday
|
| 7
|
Oct 26
|
Term Test on Tuesday, Dijkstra Handout,Thursday,HW5
|
| 8
|
Nov 2
|
Tuesday, Tutorial Handout, Thursday, HW6, Sunday November 8 is the last day to drop this class
|
| 9
|
Nov 9
|
Monday-Tuesday is UofT Fall Break, Thursday, HW7
|
| 10
|
Nov 16
|
Tuesday, Thursday, HW8
|
| 11
|
Nov 23
|
Tuesday, Thursday, HW9
|
| 12
|
Nov 30
|
Tuesday, Thursday, HW10
|
| 13
|
Dec 7
|
Tuesday, FibonacciFormula.pdf, semester ends on Wednesday - no class Thursday
|
| F
|
Dec 11-22
|
The Final Exam
|
| Register of Good Deeds
|

Add your name / see who's in!
|
|
|
This assignment is due at the tutorials on Thursday December 3. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if the teaching assistants will be having hard time deciphering your work they will give up and assume it is wrong.
Reread sections 6.1-6.2 of our textbook, and your notes for November 26 and December 1. Remember that reading math isn't like reading a novel! If you read a novel and miss a few details most likely you'll still understand the novel. But if you miss a few details in a math text, often you'll miss everything that follows. So reading math takes reading and rereading and rerereading and a lot of thought about what you've read. Also, preread chapter 7, just to get a feel for the future.
Solve problems 2abde, 2c, 4abc, 4d, 12, 16, 20, and 25 in section 6.1 and problems 1, 2, 11abcd, 11e, 30, 32, and 43 in section 6.2, but submit only your solutions of the underlined problems.
In addition, solve the following problem. There is no need to submit your solution.
Part 1. For  , let
, let  be the
be the  'th Catalan number, defined as the number of words made of
'th Catalan number, defined as the number of words made of 
 's and
's and 
 's in which in every initial segment there are at least as many
's in which in every initial segment there are at least as many  's as
's as  's. Prove that for
's. Prove that for  ,
,  .
.
Hint. If  is such a word, let
is such a word, let  be the smallest such that if you cut
be the smallest such that if you cut  after
after  letters, then the number of
letters, then the number of  's before the cut is equal to the number of
's before the cut is equal to the number of  's before the cut. What can you say about the part of
's before the cut. What can you say about the part of  before the cut, and the part of
before the cut, and the part of  after the cut?
after the cut?
Part 2. For  , let
, let  be the number of different ways of computing the product
be the number of different ways of computing the product  of
of  matrices. Prove that for
matrices. Prove that for  ,
,  .
.
Hint. In the last matrix multiplication to be carried out, you'd be multiplying the product of  of the matrices with the product of
of the matrices with the product of  of the matrices.
of the matrices.
Part 3. Let  and for
and for  let
let  be the number of triangulations of a convex
be the number of triangulations of a convex  -gon using non-crossing diagonals. Prove that for
-gon using non-crossing diagonals. Prove that for  ,
,  .
.
Hint. Choose one edge of the  -gon, and consider the triangle on top of it, what's to its left, and what's to its right.
-gon, and consider the triangle on top of it, what's to its left, and what's to its right.
Part 4. Use the above three assertions to prove that for any  ,
,  .
.
|
|
Dror's notes above / Students' notes below
|
|
Homework Assignment 9 Solution
2) Build a generating function for  , the number of integer solutions to the following equations.
, the number of integer solutions to the following equations.
c)  even
even  odd.
odd.
A) For  and
and  together, we have
together, we have 
For  , we have
, we have 
For  , we have
, we have 
In total, we have 
4 d) Three different boxes with at most five objects in the first box
A)  with
with 
For  , we have
, we have 
Note that for the other two, we don't have a limit, so:

so, in total we have: 
16) Find a generating function for the number of integers between 0 and 999,999 whose sum of digits is  .
.
A) For each integer in the range, we can express them as a six digit number, including 0's in the front (5 will be 000005).
So this amounts to finding:

So, we have 
Section 6.1 2) Find the coefficient of  in
in 
A)

The coefficient of  in this will be of
in this will be of  in
in  , which is
, which is

Scanned Solution to Homework9 P11e,32,43 in Secton6.2