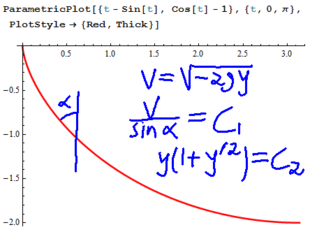| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
Monday: Separated equations, escape velocities. HW1. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
Monday: Solving exact equations, integration factors. HW2. Tuesday: Statement of the Fundamental Theorem. Class Photo. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
Monday: Last notes on the fundamental theorem. HW3. Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 2: Deriving Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
Monday: Euler and improved Euler. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
Monday: Multiple roots, reduction of order, undetermined coefficients. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
Monday: The basic properties of matrix exponentiation. Tuesday: Matrix exponentiation: examples. Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
Monday: Non-homogeneous systems. Tuesday: The Catalan numbers, power series, and ODEs. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7. Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math].
|
| 11
|
Nov 19
|
Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence. Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (tutorial): Regular singular points. HW8. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
Monday: More Sturm comparisons, changing the independent variable. Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|
Add your name / see who's in!
|
|
|
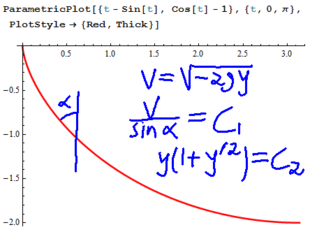
Disclamer: This is a student prepared note based on the lecure of Tuesday October 2nd.
For a function [math]\displaystyle{ y(x) }[/math] defined on [math]\displaystyle{ [a, b] }[/math] to be an extremum of [math]\displaystyle{ J(y) = \int_a^b F(x, y, y') dx }[/math], it must be that for any function [math]\displaystyle{ h(x) }[/math] defined on [math]\displaystyle{ [a, b] }[/math] that preserves the endpoints of [math]\displaystyle{ y }[/math] (that is, [math]\displaystyle{ h(a) = 0 }[/math] and [math]\displaystyle{ h(b) = 0 }[/math]), we have [math]\displaystyle{ \frac{d}{d \epsilon } J(y + \epsilon h) }[/math][math]\displaystyle{ |_{\epsilon = 0} = 0 }[/math].
[math]\displaystyle{ \frac{d}{d \epsilon } J(y + \epsilon h) }[/math][math]\displaystyle{ |_{\epsilon = 0} }[/math]
[math]\displaystyle{ = \frac{d}{d \epsilon } \int_a^b F(x, y + \epsilon h, y' + \epsilon h') dx |_{\epsilon = 0} }[/math]
Let [math]\displaystyle{ F_n }[/math] signify F differentiated with respect to its nth variable.
[math]\displaystyle{ = \int_a^b (F_1 \cdot 0 + F_2 \cdot h + F_3 \cdot h') dx |_{\epsilon = 0} }[/math]
[math]\displaystyle{ = \int_a^b (F_2(x, y, y') \cdot h + F_3(x, y, y') \cdot h') dx }[/math]
[math]\displaystyle{ = \int_a^b (F_2 \cdot h - [\frac{d}{dx} F_3] \cdot h) dx + F_3 \cdot h |_a^b }[/math] (integrating by parts)
Due to the constraints of [math]\displaystyle{ h(a) = 0 }[/math] and [math]\displaystyle{ h(b) = 0 }[/math], [math]\displaystyle{ F_3 \cdot h |_a^b = 0 }[/math].
[math]\displaystyle{ = \int_a^b (F_2 - \frac{d}{dx} F_3) \cdot h dx }[/math]
As this must be equal to 0 for all h satisfying the endpoint constraints, we must have that [math]\displaystyle{ F_2 = \frac{d}{dx} F_3 }[/math], or in other terms, [math]\displaystyle{ F_y - \frac{d}{dx} F_y' = 0 }[/math].
Special cases (without derivations):
In the case that F does not depend on y', we have [math]\displaystyle{ F_y = 0 }[/math]
In the case that F does not depend on y, we have [math]\displaystyle{ F_{y'} = c }[/math]
In the case that F does not depend on x, we have [math]\displaystyle{ F - y'F_{y'} = c }[/math]
