| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
Monday: Separated equations, escape velocities. HW1. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
Monday: Solving exact equations, integration factors. HW2. Tuesday: Statement of the Fundamental Theorem. Class Photo. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
Monday: Last notes on the fundamental theorem. HW3. Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 2: Deriving Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
Monday: Euler and improved Euler. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
Monday: Multiple roots, reduction of order, undetermined coefficients. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
Monday: The basic properties of matrix exponentiation. Tuesday: Matrix exponentiation: examples. Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
Monday: Non-homogeneous systems. Tuesday: The Catalan numbers, power series, and ODEs. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7. Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math].
|
| 11
|
Nov 19
|
Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence. Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (tutorial): Regular singular points. HW8. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
Monday: More Sturm comparisons, changing the independent variable. Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|
Add your name / see who's in!
|
|
|
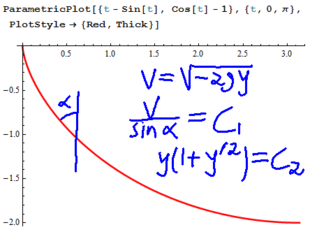
This assignment is due at the tutorial on Tuesday September 25. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong.
Question 1. Show that if [math]\displaystyle{ y=y_1(x) }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=0 }[/math], and [math]\displaystyle{ y=y_2(x) }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math], then for any constant [math]\displaystyle{ c }[/math], [math]\displaystyle{ y=cy_1+y_2 }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math].
Question 2. Solve the following differential equations
- For [math]\displaystyle{ x\gt 0 }[/math], [math]\displaystyle{ xy'+2y=\sin x }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{1}{e^y-x} }[/math] with [math]\displaystyle{ y(1)=0 }[/math]; you may want to solve for [math]\displaystyle{ x }[/math] first.
- [math]\displaystyle{ xy'=\sqrt{1-y^2} }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{x-e^{-x}}{y+e^y} }[/math].
- [math]\displaystyle{ xdx+ye^{-x}dy=0 }[/math], with [math]\displaystyle{ y(0)=1 }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{ay+b}{cx+d} }[/math], where [math]\displaystyle{ a,b,c,d }[/math] are arbitrary constants.
- [math]\displaystyle{ \frac{dy}{dx}=-\frac{ax+by}{bx+cy} }[/math], where [math]\displaystyle{ a,b,c }[/math] are arbitrary constants.
- [math]\displaystyle{ 0=(e^x\sin y + 3y)dx + (3(x+y)+e^x\cos y)dy }[/math].
Disclamer: The solutions below are by students, for students.
Solutions to HW1: page 1, page 2, page 3, page 4 Mathstudent
Solution to Question 1. Twine
Take y defined by [math]\displaystyle{ y=cy_1+y_2 }[/math] and plug it into [math]\displaystyle{ y'+p(x)y=g(x) }[/math]. We get
[math]\displaystyle{ (cy_1 + y_2)' + p(x)(cy_1 + y_2) = g(x) }[/math]
[math]\displaystyle{ c(y_1' + p(x)y_1) + (y_2' + p(x)y_2) = g(x) }[/math]
Based on our assumptions about [math]\displaystyle{ y_1 }[/math] and [math]\displaystyle{ y_2 }[/math], we have [math]\displaystyle{ y_1' + p(x)y_1 = 0 }[/math] and we have [math]\displaystyle{ y_2' + p(x)y_2 = g(x) }[/math], and so the above equation holds [math]\displaystyle{ \forall c \in \mathbb{R} }[/math].
Hence, [math]\displaystyle{ \forall c \in \mathbb{R} }[/math], [math]\displaystyle{ cy_1 + y_2 }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math].
