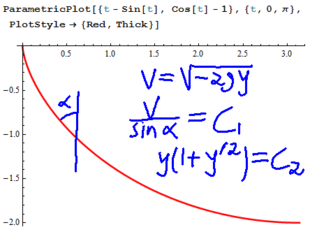12-267/Tuesday September 11 Notes

DBN: Classes: 2012-13: 12-267 / Navigation Additions to this web site no longer count towards good deed points. # Week of... Notes and Links 1 Sep 10 About This Class.  Monday: Introduction and the Brachistochrone.  Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes.  Friday: Some basic techniques: first order linear equations. 2 Sep 17  Monday: Separated equations, escape velocities. HW1.  Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations.  Friday: Reverse engineering separated and exact equations. 3 Sep 24  Monday: Solving exact equations, integration factors. HW2.  Tuesday: Statement of the Fundamental Theorem. Class Photo.  Friday: Proof of the Fundamental Theorem. 4 Oct 1  Monday: Last notes on the fundamental theorem. HW3.  Tuesday Hour 1: The chain law, examples of variational problems.  Tuesday Hour 2: Deriving Euler-Lagrange.  Friday: Reductions of Euler-Lagrange. 5 Oct 8 Monday is thanksgiving.  Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4.  Friday: More Lagrange multipliers, numerical methods. 6 Oct 15  Monday: Euler and improved Euler.  Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods.  Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs. 7 Oct 22  Monday: Multiple roots, reduction of order, undetermined coefficients.  Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday. 8 Oct 29  Monday: The basic properties of matrix exponentiation.  Tuesday: Matrix exponentiation: examples.  Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class 9 Nov 5  Monday: Non-homogeneous systems.  Tuesday: The Catalan numbers, power series, and ODEs.  Friday: Global existence for linear ODEs, the Wronskian. 10 Nov 12 Monday-Tuesday is UofT November break. HW7.  Friday: Series solutions for $y'=f(x,y)$. 11 Nov 19  Monday: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} is irrational, more on the radius of convergence.  Tuesday (class): Airy's equation, Fuchs' theorem.  Tuesday (tutorial): Regular singular points. HW8.  Friday: Discussion of regular singular points.. 12 Nov 26  Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF).  Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9.  Friday: Non-oscillation, Sturm comparison. 13 Dec 3  Monday: More Sturm comparisons, changing the independent variable.  Tuesday: Amplitudes of oscillations. Last class was on Tuesday! F1 Dec 10 F2 Dec 17 The Final Exam (time, place, style, office hours times) Register of Good Deeds Add your name / see who's in!

Solving the complicated integral in the Brachistochroe integral

$\int {\sqrt {\frac {d-y}{y}}}dy$

$=\int {\sqrt {\frac {dy-y^{2}}{y}}}dy$

Complete the square in the integrand:

$=\int {\sqrt {\frac {{\frac {d^{2}}{4}}-(y-{\frac {d}{2}})^{2}}{y}}}$

Substitute $u=y-{\frac {d}{2}}$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle du = dy } :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \int 2 \sqrt{\frac{\frac{d^2}{4} - u^2}{d+2 u}} du }

Assuming all variables are positive, substitute $u={\frac {1}{2}}d\sin {s}$ and $du={\frac {1}{2}}d\cos {s}ds$. Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\frac{d^2}{4} - u^2} = \sqrt{\frac{d^2}{4} - \frac{1}{4} d^2 \sin^2{s}} = \frac{1}{2} d \cos{s}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = \sin^{-1}{\frac{2u}{d}}} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{d^2}{2} \int \frac{\cos^2{s}}{d \sin{s} + d} ds}

For the integrand substitute $p=\tan {\frac {s}{2}}$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dp = \frac{1}{2} \sec^2{\frac{s}{2}} ds} . Then transform the integrand using the substitutions $\sin {s}={\frac {2p}{p^{2}+1}}$, $\cos {s}={\frac {1-p^{2}}{p^{2}+1}}$ and $ds={\frac {2dp}{p^{2}+1}}$:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{d^2}{2} \int 2 \frac{(1-p^2)^2}{(p^2 + 1)^3 (\frac{2 d p}{p^2 + 1} + d)} dp}

Simplify the integrand ${\frac {2(1-p^{2})^{2}}{(p^{2}+1)^{3}({\frac {2dp}{p^{2}+1}}+d)}}$ to get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2 (p-1)^2}{d p^4 + 2 d p^2 + d}} :

$={\frac {d^{2}}{2}}\int {\frac {2(p-1)^{2}}{dp^{4}+2dp^{2}+d}}dp$

$=d^{2}\int {\frac {(p-1)^{2}}{dp^{4}+2dp^{2}+d}}dp$

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = d^2 \int \frac{(p-1)^2}{d (p^2+1)^2} dp }

$=d\int {\frac {(p-1)^{2}}{(p^{2}+1)^{2}}}dp$

For the integrand ${\frac {(p-1)^{2}}{(p^{2}+1)^{2}}}$ use partial fractions:

$=d\int ({\frac {1}{p^{2}+1}}-{\frac {2p}{(p^{2}+1)^{2}}})dp$

$=d\int {\frac {1}{(p^{2}+1)}}dp-2d\int {\frac {p}{(p^{2}+1)^{2}}}dp$

For the integrand ${\frac {p}{(p^{2}+1)^{2}}}$, substitute $w=p^{2}+1$ and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dw = 2 p dp} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = d \int \frac{1}{p^2+1} dp - d \int \frac{1}{w^2} dw }

The integral of ${\frac {1}{p^{2}+1}}$ is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan^{-1}{p}} :

$=d\tan ^{-1}{p}-d\int {\frac {1}{w^{2}}}dw$

$=d\tan ^{-1}{p}+{\frac {d}{w}}+constant$

Substitute back for $w=p^{2}+1$:

$={\frac {d((p^{2}+1)tan^{-1}{p}+1)}{p^{2}+1}}+C$

Substitute back for $p=\tan {\frac {s}{2}}$:

$={\frac {1}{2}}d(\cos {s}+2\tan ^{-1}{\tan {\frac {s}{2}}}+1)+C$

Substitute back for $s=\sin ^{-1}{\frac {2u}{d}}$:

$=1/2({\sqrt {d^{2}-4u^{2}}}+2d\tan ^{-1}({\frac {2u}{d{\sqrt {1-{\frac {4u^{2}}{d^{2}}}}}+1)}})+d)+C$

Substitute back for $u=y-{\frac {d}{2}}$:

$=d(-\tan ^{-1}{\frac {d-2y}{2d{\sqrt {\frac {y(d-y)}{d^{2}}}}+d}})+{\sqrt {y(d-y)}}+{\frac {d}{2}}+C$

Factor the answer a different way:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} (-2 d \tan^{-1}{\frac{d-2 y}{2 d \sqrt{\frac{y (d-y)}{d^2}}+d}}+2 \sqrt{y (d-y)}+d)+C}

Which is equivalent for restricted y and d values to:

$=y{\sqrt {{\frac {d}{y}}-1}}-{\frac {1}{2}}d\tan ^{-1}{\frac {{\sqrt {{\frac {d}{y}}-1}}(d-2y)}{2(d-y)}}+C$

Syjytg 23:00, 11 September 2012 (EDT)