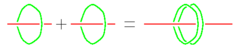The Existence of the Exponential Function

Paperlets Navigation Panel   Algebraic Knot Theory Algebraic Knot Theory - A Call for Action. The Kontsevich Integral for Knotted Trivalent Graphs. Knotted Trivalent Graphs are Finitely Presented. VS, TS and TG Algebras. The Alexander Polynomial of a Knotted Trivalent Graph. Some Questions About Trinions. Finite Type Invariants The Envelope of a Finite Type Invariant. The Envelope of The Alexander Polynomial. Some Quotients of A. Associators with Frozen Feet. The HOMFLY Braidor Algebra. Coloured Chord Diagrams. Khovanov Homology Mutation Invariance of Khovanov Homology. Khovanov Homology of Alternating Tangles. Other The Existence of the Exponential Function. The Many Faces of Alexander.

Introduction

The purpose of this paperlet is to use some homological algebra in order to prove the existence of a power series Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e(x)} (with coefficients in ${\mathbb {Q} }$) which satisfies the non-linear equation

[Main]

$e(x+y)=e(x)e(y)$

as well as the initial condition

[Init]

$e(x)=1+x+$(higher order terms).

Alternative proofs of the existence of $e(x)$ are of course available, including the explicit formula $e(x)=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}$. Thus the value of this paperlet is not in the result it proves but rather in the allegorical story it tells: that there is a technique to solve functional equations such as [Main] using homology. There are plenty of other examples for the use of that technique, in which the equation replacing [Main] isn't as easy (see Further Examples below). Thus the exponential function seems to be the easiest illustration of a general principle and as such it is worthy of documenting.

Thus below we will pretend not to know the exponential function and/or its relationship with the differential equation $e'=e$.

Acknowledgment

Significant parts of this paperlet were contributed by Omar Antolin Camarena.

The Scheme

We aim to construct $e(x)$ and solve [Main] inductively, degree by degree. Equation [Init] gives $e(x)$ in degrees 0 and 1, and the given formula for $e(x)$ indeed solves [Main] in degrees 0 and 1. So booting the induction is no problem. Now assume we've found a degree 7 polynomial $e_{7}(x)$ which solves [Main] up to and including degree 7, but at this stage of the construction, it may well fail to solve [Main] in degree 8. Thus modulo degrees 9 and up, we have

[M]

$e_{7}(x+y)-e_{7}(x)e_{7}(y)=M(x,y)$,

where $M(x,y)$ is the "mistake for $e_{7}$", a certain homogeneous polynomial of degree 8 in the variables $x$ and $y$.

Our hope is to "fix" the mistake $M$ by replacing $e_{7}(x)$ with $e_{8}(x)=e_{7}(x)+\epsilon (x)$, where $\epsilon (x)$ is a degree 8 "correction", a homogeneous polynomial of degree 8 in $x$ (well, in this simple case, just a multiple of $x^{8}$).

*1 The terms containing no $\epsilon$'s make a copy of the left hand side of [M]. The terms linear in $\epsilon$ are $\epsilon (x+y)$, $-e_{7}(x)\epsilon (y)$ and $-\epsilon (x)e_{7}(y)$. Note that since the constant term of $e_{7}$ is 1 and since we only care about degree 8, the last two terms can be replaced by $-\epsilon (y)$ and $-\epsilon (x)$, respectively. Finally, we don't even need to look at terms higher than linear in $\epsilon$, for these have degree 16 or more, high in the stratosphere.

So we substitute $e_{8}(x)=e_{7}(x)+\epsilon (x)$ into $e(x+y)-e(x)e(y)$ (a version of [Main]), expand, and consider only the low degree terms - those below and including degree 8:^*1

$e_{8}(x+y)-e_{8}(x)e_{8}(y)=M(x,y)-\epsilon (y)+\epsilon (x+y)-\epsilon (x)$.

We define a "differential" $d:{\mathbb {Q} }[x]\to {\mathbb {Q} }[x,y]$ by $(df)(x,y)=f(y)-f(x+y)+f(x)$, and the above equation becomes

$e_{8}(x+y)-e_{8}(x)e_{8}(y)=M(x,y)-(d\epsilon )(x,y)$.

*2 It is worth noting that in some a priori sense the existence a solution of $e(x+y)=e(x)e(y)$ is unexpected. For $e$ must be an element of the relatively small space ${\mathbb {Q} }[[x]]$ of power series in one variable, but the equation it is required to satisfy lives in the much bigger space ${\mathbb {Q} }[[x,y]]$ of power series in two variables. Thus in some sense we have more equations than unknowns and a solution is unlikely. How fortunate we are that exponentials do exist, after all!

To continue with our inductive construction we need to have that $e_{8}(x+y)-e_{8}(x)e_{8}(y)=0$. Hence the existence of the exponential function hinges upon our ability to find an $\epsilon$ for which $M=d\epsilon$. In other words, we must show that $M$ is in the image of $d$. This appears hopeless unless we learn more about $M$, for the domain space of $d$ is much smaller than its target space and thus $d$ cannot be surjective, and if $M$ was in any sense "random", we simply wouldn't be able to find our correction term $\epsilon$.^*2

As we shall see momentarily by "finding syzygies", $\epsilon$ and $M$ fit within the 1st and 2nd chain groups of a rather short complex

$\left(\epsilon \in C^{1}={\mathbb {Q} }[[x]]\right)\longrightarrow \left(M\in C^{2}={\mathbb {Q} }[[x,y]]\right)\longrightarrow \left(C^{3}={\mathbb {Q} }[[x,y,z]]\right)$,

whose first differential was already written and whose second differential is given by $(d^{2}m)(x,y,z)=m(y,z)-m(x+y,z)+m(x,y+z)-m(x,y)$ for any $m\in {\mathbb {Q} }[[x,y]]$. We shall further see that for "our" $M$, we have $d^{2}M=0$. Therefore in order to show that $M$ is in the image of $d^{1}$, it suffices to show that the kernel of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^2} is equal to the image of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^1} , or simply that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^2=0} .

Finding a Syzygy

So what kind of relations can we get for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} ? Well, it measures how close Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_7} is to turning sums into products, so we can look for preservation of properties that both addition and multiplication have. For example, they're both commutative, so we should have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(x,y)=M(y,x)} , and indeed this is obvious from the definition. Now let's try associativity, that is, let's compute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_7(x+y+z)} associating first as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x+y)+z} and then as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x+(y+z)} . In the first way we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_7(x+y+z) = M(x+y,z)+e_7(x+y)e_7(z) = M(x+y,z)+\left(M(x,y)+e_7(x)e_7(y)\right)e_7(z)} .

In the second we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_7(x+y+z) = M(x,y+z)+e_7(x)e_7(y+z) = M(x+y,z)+e_7(x)\left(M(y,z)+e_7(y)e_7(z)\right)} .

Comparing these two we get an interesting relation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(x+y,z)+M(x,y)e_7(z) = M(x,y+z) + e_7(x)M(y,z) } . Since we'll only use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} to find the next highest term, we can be sloppy about all but the first term of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} . This means that in the relation we just found we can replace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_7} by its constant term, namely 1. Upon rearranging, we get the relation promised for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^2M = M(y,z)-M(x+y,z)+M(x,y+z)-M(x,y) = 0} .

Computing the Homology, Easy but Limited

Now let's prove that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^2=0} for our (piece of) chain complex. That is, letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(x,y) \in \mathbb{Q}[[x,y]]} be such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^2M=0} , we'll prove that for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(x) \in \mathbb{Q}[[x]]} we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^1\epsilon = M } .

Write the two power series as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(x) = \sum{\frac{\alpha_i}{i!}x^i} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(x,y) = \sum{\frac{m_{ij}}{i!j!}x^i y^j} } , where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_i} are the unknowns we wish to solve for.

The coefficient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^i y^j z^k} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(y,z)-M(x+y,z)+M(x,y+z)-M(x,y)} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta_{i0} m_{jk}}{j!k!} - {{i+j} \choose i} \frac{m_{i+j,k}}{(i+j)!k!} + {{j+k} \choose j} \frac{m_{i,j+k}}{i!(j+k)!} - \frac{\delta_{k0} m_{ij}}{i!j!}} .

Here, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{i0} } is a Kronecker delta: 1 if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=0 } and 0 otherwise. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^2 M = 0 } , this coefficient is zero. Multiplying by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i!j!k! } (and noting that, for example, the first term doesn't need an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i! } since the delta is only nonzero when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=0 } ) we get:

[m]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{i0} m_{jk} - m_{i+j,k} + m_{i,j+k} + \delta_{k0} m_{ij}=0} .

An entirely analogous procedure tells us that the equations we must solve boil down to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{i0} \alpha_j - \alpha_{i+j} + \delta_{j0} \alpha_i = m_{ij} } .

By setting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=j=0 } in this last equation we see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_0 = m_{00} } . Now let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} be arbitrary positive integers. This solves for most of the coefficients: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{i+j}=-m_{ij}} . Any integer at least two can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i+j } , so this determines all of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_m } for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \ge 2 } . We just need to prove that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_m } is well defined, that is, that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{i+j}=-m_{ij}} doesn't depend on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } but only on their sum.

But when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } are strictly positive, the relation [m] reads Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{i+j,k} = m_{i,j+k} } , which show that we can "transfer" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } from one index to the other, which is what we wanted.

It only remains to find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 } but it's easy to see this is impossible: if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^1\epsilon = M } , then so does Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(x)+kx } for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } , so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 } is arbitrary. How do our coefficient equations tell us this?

Well, we can't find a single equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 } ! We've already tried taking both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } to be zero, and also taking them both positive. We only have taking one zero and one positive left. Doing so gives two necessary conditions for the existence of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_m } : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{0r} = m_{r0} = 0 } for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r>0 } . So no Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 } comes up, and we're still not done. Fortunately setting one of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } to be zero and one positive in the realtion for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{ij} } does the trick.

Computing the Homology, Hard but Rewarding

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_n^k} denote the space of degree n polynomials in (commuting) variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1,\ldots,x_k} and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^k:C_n^k\to C_n^{k+1}} be defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^k=\sum_{i=0}^{k+1}(-)^i d^k_i} , where

Further Examples

Let us briefly list a number of other places in mathematics where similar "non-linear algebraic functional equations" need to be solved. The techniques we have developed to solve [Main] can be applied in all of those cases, though sometimes it is fully successful and sometimes something breaks down somewhere along the way.

In knot theory solving this equations is as easy as calculating 1+1=2 on an abacus: See [Bar-Natan_Le_Thurston_03].

The "Duflo Homomorphism" Equation

This is the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\Delta\otimes 1)\Upsilon = \Upsilon^{12}\Upsilon^{23}} ,

written in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(S(L^\star)_L\otimes S(L^\star)_L\otimes U(L)\right)^L} , for an unknown Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Upsilon\in \left(S(L^\star)_L\otimes U(L)\right)^L} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} is a Lie algebra. With appropriate qualifications, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(L^\star)\otimes U(L)=\operatorname{Hom}(S(L),U(L))} , and our equation becomes the statement "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Upsilon} is an algebra homomorphism between the invariants of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(L)} and the invariants of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(L)} ", and its solution is the so-called "Duflo homomorphism". This is a typical "homomorphism wanted" equation and it it has many relatives, including our primary example Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e(x+y)=e(x)e(y)} which is also known as the statement "the additive group of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb R}} is isomorphic to the multiplicative group of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb R}_+} ". Note that in general, the equation for being a homomorphism, say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi(xy)=\varphi(x)\varphi(y)} , is non-linear in the homomorphism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} itself.

Where from cometh the syzygies? As in the case of the exponential function, they come from the fact that for a homomorphism, associativity in the target follows from associativity in the domain.

The "Formal Quantization" Equation

This is the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f\star g)\star h = f\star(g\star h),}

written for an unknown "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \star} -product", within a certain complicated space of "potential products" which resembles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{Hom}(V\otimes V,V)} or $V^{\star }\otimes V^{\star }\otimes V$ for some vector space $V$. This is a typical "algebraic structure wanted" equation, in which the unknown is an "algebraic structure" (an associative product $\star$, in this case) and the equation is "the structure satisfies a law" (the associative law, in our case). Note that algebraic laws are often non-linear in the structure that they govern (the example relevant here is that the associative law is "quadratic as a function of the product"). Other examples abound, with the "structure" replaced by a "bracket" or anything else, and the "law" replaced by "Jacobi's equation" or whatever you fancy.

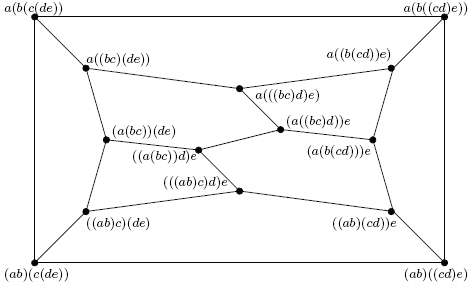
Where from cometh the syzygies? From the pentagon shown on the right.

The Drinfel'd Pentagon Equation

This is the equation

$\Phi (t^{12},t^{23})\Phi (t^{12}+t^{13},t^{24}+t^{34})\Phi (t^{23},t^{34})=\Phi (t^{13}+t^{23},t^{34})\Phi (t^{12},t^{24}+t^{34})$.

It is an equation written in some strange non-commutative algebra ${\mathcal {A}}_{4}^{h}$, for an unknown "function" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(a,b)} which in itself lives in some non-commutative algebra Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}^h_3} . This equation is related to tensor categories, to quasi-Hopf algebras and (strange as it may seem) to knot theory, and is commonly summarized by either of the following two pictures:

This equation is a close friend of the Drinfel'd Hexagon Equation, and you can read more about both of them at [Drinfeld_90], [Drinfeld_91] and [Bar-Natan_97]. These equations have many relatives living in many further exotic spaces.

Where from cometh the syzygies? Here the equations come from the pentagon, so the syzygies must come from somewhere more complicated - the "Stasheff Polyhedron":

The Drinfel'd Twist Equation

This is the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi'(x,y,z)=F^{-1}(x+y,z)F^{-1}(x,y)\Phi F(y,z)F(x,y+z)} .

This equation is written in another strange non-commutative algebra Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}_3} , which is a superset of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}^h_3} . The unknown Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} lives in some space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}_2} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi'} are solutions of the Drinfel'd pentagon of before. You can read more about this equation at [Drinfeld_90], [Drinfeld_91] and [Le_Murakami_96]. This equation has many relatives living in many further exotic spaces.

Where from cometh the syzygies? Again from the pentagon, but in a different way.

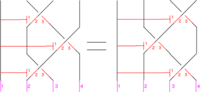
The Braidor Equation

This is the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x_1,x_2,x_3) B(x_1+x_3,x_2,x_4) B(x_1,x_3,x_4)} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x_1+x_2,x_3,x_4) B(x_1,x_2,x_4) B(x_1+x_4,x_2,x_3)} ,

written in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}_4} for an unknown Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\in{\mathcal A}_3} . It is related to the picture on the right and through it to the third Reidemeister move of braid theory and knot theory. At present, the only place to read more about it is 06-1350/Homework Assignment 4.

Where from cometh the syzygies? The third Reidemeister move comes from resolving a triple point. The corresponding syzygy comes from resolving a quadruple point. See a picture at 06-1350/Homework Assignment 4.

Further Further Examples

This subsection is by definition forever empty, for if a worthwhile further further example comes to mind, mine or yours, it should be added as a subsection right above.

References

[Bar-Natan_97] ^  D. Bar-Natan, Non-associative tangles, in Geometric topology (proceedings of the Georgia international topology conference), (W. H. Kazez, ed.), 139-183, Amer. Math. Soc. and International Press, Providence, 1997.

[Bar-Natan_Le_Thurston_03] ^  D. Bar-Natan, T. Q. T. Le and D. P. Thurston, Two applications of elementary knot theory to Lie algebras and Vassiliev invariants, Geometry and Topology 7-1 (2003) 1-31, arXiv:math.QA/0204311.

[Drinfeld_90] ^  V. G. Drinfel'd, Quasi-Hopf algebras, Leningrad Math. J. 1 (1990) 1419-1457.

[Drinfeld_91] ^  V. G. Drinfel'd, On quasitriangular Quasi-Hopf algebras and a group closely connected with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{Gal}(\bar{\mathbb Q}/{\mathbb Q})} , Leningrad Math. J. 2 (1991) 829-860.

[Le_Murakami_96] ^  T. Q. T. Le and J. Murakami, The universal Vassiliev-Kontsevich invariant for framed oriented links, Compositio Math. 102 (1996), 41-64, arXiv:hep-th/9401016.