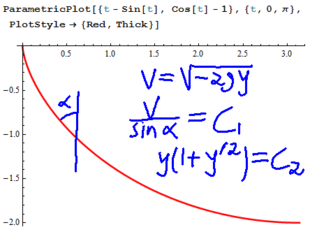12-267/Homework Assignment 1: Difference between revisions
No edit summary |
Mathstudent (talk | contribs) No edit summary |
||
| Line 14: | Line 14: | ||
# <math>\frac{dy}{dx}=-\frac{ax+by}{bx+cy}</math>, where <math>a,b,c</math> are arbitrary constants. |
# <math>\frac{dy}{dx}=-\frac{ax+by}{bx+cy}</math>, where <math>a,b,c</math> are arbitrary constants. |
||
# <math>0=(e^x\sin y + 3y)dx + (3(x+y)+e^x\cos y)dy</math>. |
# <math>0=(e^x\sin y + 3y)dx + (3(x+y)+e^x\cos y)dy</math>. |
||
[http://drorbn.net/index.php?title=Image:001.jpg Solution to HW1, page 1] [[User:Mathstudent|Mathstudent]] |
|||
[http://drorbn.net/index.php?title=Image:002.jpg Solution to HW1, page 2] [[User:Mathstudent|Mathstudent]] |
|||
[http://drorbn.net/index.php?title=Image:003.jpg Solution to HW1, page 3] [[User:Mathstudent|Mathstudent]] |
|||
[http://drorbn.net/index.php?title=Image:004.jpg Solution to HW1, page 4] [[User:Mathstudent|Mathstudent]] |
|||
Revision as of 18:22, 23 October 2012
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due at the tutorial on Tuesday September 25. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong.
Question 1. Show that if [math]\displaystyle{ y=y_1(x) }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=0 }[/math], and [math]\displaystyle{ y=y_2(x) }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math], then for any constant [math]\displaystyle{ c }[/math], [math]\displaystyle{ y=cy_1+y_2 }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math].
Question 2. Solve the following differential equations
- For [math]\displaystyle{ x\gt 0 }[/math], [math]\displaystyle{ xy'+2y=\sin x }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{1}{e^y-x} }[/math] with [math]\displaystyle{ y(1)=0 }[/math]; you may want to solve for [math]\displaystyle{ x }[/math] first.
- [math]\displaystyle{ xy'=\sqrt{1-y^2} }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{x-e^{-x}}{y+e^y} }[/math].
- [math]\displaystyle{ xdx+ye^{-x}dy=0 }[/math], with [math]\displaystyle{ y(0)=1 }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{ay+b}{cx+d} }[/math], where [math]\displaystyle{ a,b,c,d }[/math] are arbitrary constants.
- [math]\displaystyle{ \frac{dy}{dx}=-\frac{ax+by}{bx+cy} }[/math], where [math]\displaystyle{ a,b,c }[/math] are arbitrary constants.
- [math]\displaystyle{ 0=(e^x\sin y + 3y)dx + (3(x+y)+e^x\cos y)dy }[/math].
Solution to HW1, page 1 Mathstudent Solution to HW1, page 2 Mathstudent Solution to HW1, page 3 Mathstudent Solution to HW1, page 4 Mathstudent