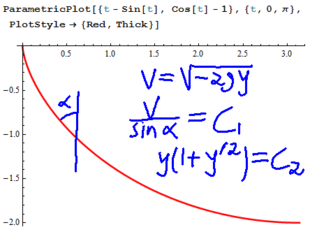|
|
| Line 33: |
Line 33: |
|
|
|
|
|
[http://graphics.ethz.ch/teaching/former/vc_master_06/Downloads/viscomp-varcalc_6.pdf Useful PDF: proof of Euler-Lagrange equation, explanation, examples ] [[User:Vsbdthrsh|Vsbdthrsh]] |
|
[http://graphics.ethz.ch/teaching/former/vc_master_06/Downloads/viscomp-varcalc_6.pdf Useful PDF: proof of Euler-Lagrange equation, explanation, examples ] [[User:Vsbdthrsh|Vsbdthrsh]] |
|
|
|
|
|
[http://drorbn.net/index.php?title=12-267/Euler%27s_Method Python example for Euler's Method] [[User:Twine:Twine]] |
|
|
|
|
|
[http://math.hunter.cuny.edu/mbenders/cofv.pdf In-depth coverage of Calculus of Variations] |
|
[http://math.hunter.cuny.edu/mbenders/cofv.pdf In-depth coverage of Calculus of Variations] |
Revision as of 10:43, 15 October 2012
| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Monday: Introduction and the Brachistochrone.  Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes.  Friday: Some basic techniques: first order linear equations. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
 Monday: Separated equations, escape velocities. HW1. Monday: Separated equations, escape velocities. HW1.  Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations.  Friday: Reverse engineering separated and exact equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
 Monday: Solving exact equations, integration factors. HW2. Monday: Solving exact equations, integration factors. HW2.  Tuesday: Statement of the Fundamental Theorem. Class Photo. Tuesday: Statement of the Fundamental Theorem. Class Photo.  Friday: Proof of the Fundamental Theorem. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
 Monday: Last notes on the fundamental theorem. HW3. Monday: Last notes on the fundamental theorem. HW3.  Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 1: The chain law, examples of variational problems.  Tuesday Hour 2: Deriving Euler-Lagrange. Tuesday Hour 2: Deriving Euler-Lagrange.  Friday: Reductions of Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving.  Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4.  Friday: More Lagrange multipliers, numerical methods. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
 Monday: Euler and improved Euler. Monday: Euler and improved Euler.  Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods.  Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
 Monday: Multiple roots, reduction of order, undetermined coefficients. Monday: Multiple roots, reduction of order, undetermined coefficients.  Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
 Monday: The basic properties of matrix exponentiation. Monday: The basic properties of matrix exponentiation.  Tuesday: Matrix exponentiation: examples. Tuesday: Matrix exponentiation: examples.  Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
 Monday: Non-homogeneous systems. Monday: Non-homogeneous systems.  Tuesday: The Catalan numbers, power series, and ODEs. Tuesday: The Catalan numbers, power series, and ODEs.  Friday: Global existence for linear ODEs, the Wronskian. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7.  Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math]. Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math].
|
| 11
|
Nov 19
|
 Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence. Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence.  Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (class): Airy's equation, Fuchs' theorem.  Tuesday (tutorial): Regular singular points. HW8. Tuesday (tutorial): Regular singular points. HW8.  Friday: Discussion of regular singular points.. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
 Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF).  Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9.  Friday: Non-oscillation, Sturm comparison. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
 Monday: More Sturm comparisons, changing the independent variable. Monday: More Sturm comparisons, changing the independent variable.  Tuesday: Amplitudes of oscillations. Last class was on Tuesday! Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|

Add your name / see who's in!
|
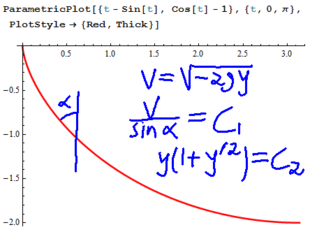
|
|
Advanced Ordinary Differential Equations
Department of Mathematics, University of Toronto, Fall 2012
Agenda: If calculus is about change, differential equations are the equations governing change. We'll learn much about these, and nothing's more important!
Instructor: Dror Bar-Natan, drorbn@math.toronto.edu, Bahen 6178, 416-946-5438. Office hours: by appointment.
Classes: Mondays, Tuesdays, and Fridays 9-10 in RW 229.
|
|
Teaching Assistant: Jordan Bell, jordan.bell@utoronto.ca.
Tutorials: Tuesdays 10-11 at RW 229. No tutorials on the first week of classes.
|
Text
Boyce and DiPrima, Elementary Differential Equations and Boundary Value Problems (current edition is 9th and 10th will be coming out shortly. Hopefully any late enough edition will do).
Further Resources
- Also previously taught by T. Bloom, C. Pugh, D. Remenik.
|
|
Dror's notes above / Student's notes below
|
|
Drorbn 06:36, 12 September 2012 (EDT): Material by Syjytg moved to 12-267/Tuesday September 11 Notes.
Summary of techniques to solve differential equations Vsbdthrsh
Fundamental Theorem and Proof from Lecture Twine
Derivation of Euler-Lagrange from Lecture Twine
Useful PDF: proof of Euler-Lagrange equation, explanation, examples Vsbdthrsh
Python example for Euler's Method User:Twine:Twine
In-depth coverage of Calculus of Variations
A good summary of what we've covered so far
Simon1
All class notes from September 10th to October 5th Simon1