|
|
| Line 1: |
Line 1: |
|
|
{{12-267/Navigation}} |
|
|
|
|
Disclamer: This is a student prepared note based on [http://drorbn.net/dbnvp/12-267-121002-2.php the lecure of Tuesday October 2nd]. |
|
Disclamer: This is a student prepared note based on [http://drorbn.net/dbnvp/12-267-121002-2.php the lecure of Tuesday October 2nd]. |
|
|
|
|
Revision as of 16:54, 24 October 2012
| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Monday: Introduction and the Brachistochrone.  Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes.  Friday: Some basic techniques: first order linear equations. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
 Monday: Separated equations, escape velocities. HW1. Monday: Separated equations, escape velocities. HW1.  Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations.  Friday: Reverse engineering separated and exact equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
 Monday: Solving exact equations, integration factors. HW2. Monday: Solving exact equations, integration factors. HW2.  Tuesday: Statement of the Fundamental Theorem. Class Photo. Tuesday: Statement of the Fundamental Theorem. Class Photo.  Friday: Proof of the Fundamental Theorem. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
 Monday: Last notes on the fundamental theorem. HW3. Monday: Last notes on the fundamental theorem. HW3.  Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 1: The chain law, examples of variational problems.  Tuesday Hour 2: Deriving Euler-Lagrange. Tuesday Hour 2: Deriving Euler-Lagrange.  Friday: Reductions of Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving.  Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4.  Friday: More Lagrange multipliers, numerical methods. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
 Monday: Euler and improved Euler. Monday: Euler and improved Euler.  Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods.  Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
 Monday: Multiple roots, reduction of order, undetermined coefficients. Monday: Multiple roots, reduction of order, undetermined coefficients.  Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
 Monday: The basic properties of matrix exponentiation. Monday: The basic properties of matrix exponentiation.  Tuesday: Matrix exponentiation: examples. Tuesday: Matrix exponentiation: examples.  Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
 Monday: Non-homogeneous systems. Monday: Non-homogeneous systems.  Tuesday: The Catalan numbers, power series, and ODEs. Tuesday: The Catalan numbers, power series, and ODEs.  Friday: Global existence for linear ODEs, the Wronskian. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7.  Friday: Series solutions for Friday: Series solutions for  . .
|
| 11
|
Nov 19
|
 Monday: Monday:  is irrational, more on the radius of convergence. is irrational, more on the radius of convergence.  Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (class): Airy's equation, Fuchs' theorem.  Tuesday (tutorial): Regular singular points. HW8. Tuesday (tutorial): Regular singular points. HW8.  Friday: Discussion of regular singular points.. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
 Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF).  Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9.  Friday: Non-oscillation, Sturm comparison. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
 Monday: More Sturm comparisons, changing the independent variable. Monday: More Sturm comparisons, changing the independent variable.  Tuesday: Amplitudes of oscillations. Last class was on Tuesday! Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|

Add your name / see who's in!
|
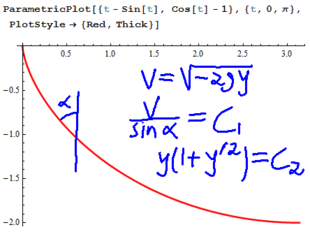
|
|
Disclamer: This is a student prepared note based on the lecure of Tuesday October 2nd.
For a function  defined on
defined on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) to be an extremum of
to be an extremum of  , it must be that for any function
, it must be that for any function  defined on
defined on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) that preserves the endpoints of
that preserves the endpoints of  (that is,
(that is,  and
and  ), we have
), we have 
 .
.



Let  signify F differentiated with respect to its nth variable.
signify F differentiated with respect to its nth variable.


![{\displaystyle =\int _{a}^{b}(F_{2}\cdot h-[{\frac {d}{dx}}F_{3}]\cdot h)dx+F_{3}\cdot h|_{a}^{b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c5e7707629c2da1c5aab926f8e5cd0cb20846b) (integrating by parts)
(integrating by parts)
Due to the constraints of  and
and  ,
,  .
.

As this must be equal to 0 for all h satisfying the endpoint constraints, we must have that  , or in other terms,
, or in other terms,  .
.



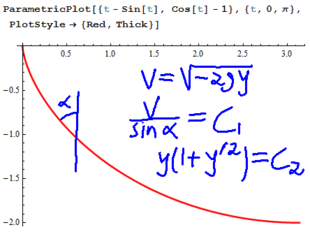

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)












![{\displaystyle =\int _{a}^{b}(F_{2}\cdot h-[{\frac {d}{dx}}F_{3}]\cdot h)dx+F_{3}\cdot h|_{a}^{b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c5e7707629c2da1c5aab926f8e5cd0cb20846b)



