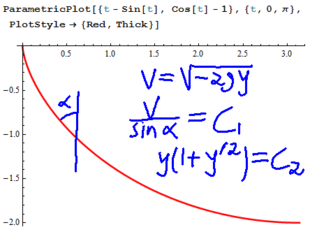12-267/Homework Assignment 6: Difference between revisions

From Drorbn
Jump to navigationJump to search
No edit summary
No edit summary
 
(9 intermediate revisions by 3 users not shown)
Line 1: Line 1:
{{12-267/Navigation}}
{{12-267/Navigation}}
{{In Preparation}}


This assignment is due in class on Friday November 9. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.
This assignment is due in class on Friday November 9. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.


'''Task 1.''' Draw the phase portraits for the following systems, near <math>(x,y)=(0,0)</math>:
'''Task 1.'''
# <math>\begin{cases} \dot{x}=2x+y \\ \dot{y}=-x+4y \end{cases}</math>.
# <math>\begin{cases} \dot{x}=4x-5y \\ \dot{y}=4x-4y \end{cases}</math>.
# <math>\begin{cases} \dot{x}=x-2y \\ \dot{y}=-2x+4y \end{cases}</math>.
# <math>\begin{cases} \dot{x}=-x+y \\ \dot{y}=-5x+3y \end{cases}</math>.
# <math>\begin{cases} \dot{x}=-5x+4y \\ \dot{y}=-8x+7y \end{cases}</math>.


'''Task 2.''' Draw the phase portrait of the system
'''Task 2.''' Draw the phase portrait of the system
Line 12: Line 16:
near the point <math>(x,y)=(1,2)</math>.
near the point <math>(x,y)=(1,2)</math>.


'''Task 3.''' Solve using diagonalization (one solution is enough):
⚫
'''Task 3.''' (Not for grade). Find a quadratic differential equation whose phase portrait is as below.
# <math>v'=\begin{pmatrix} 2 & -1 \\ 3 & -2 \end{pmatrix}v + \begin{pmatrix} e^t \\ t \end{pmatrix}</math>.
# <math>v'=\begin{pmatrix} 2 & -5 \\ 1 & -2 \end{pmatrix}v + \begin{pmatrix} -\cos t \\ \sin t \end{pmatrix}</math>.

'''Task 4.''' Assume <math>t>0</math>. For the following equation,
<center><math>tv'=\begin{pmatrix} 2 & -1 \\ 3 & -2 \end{pmatrix}v + \begin{pmatrix} 1-t^2 \\ 2t \end{pmatrix}</math></center>,
it is given that a solution of the homogeneous version is
<center><math>v(t) = c_1\begin{pmatrix}1\\1\end{pmatrix}t + \begin{pmatrix}1\\3\end{pmatrix}t^{-1}</math>.</center>
Use "fundamental solutions" to find a solution of the full equation.

⚫
'''Task 5.''' (Not for grade). Find a quadratic differential equation whose phase portrait is as below.


[[Image:12-267-MonkeySaddleFlow.png|center|400px]]
[[Image:12-267-MonkeySaddleFlow.png|center|400px]]


'''Hint.''' "Monkey Saddle".
'''Hint.''' "Monkey Saddle".

{{Template:12-267:Dror/Students Divider}}

[http://imgur.com/a/53nSl#0 Solutions] [[User:Vsbdthrsh|Vsbdthrsh]]

Solutions to HW6: [[User:Dongwoo.kang|Dongwoo.kang]]
<gallery>
Image:12-267(HW6-1).jpg|page 1
Image:12-267(HW6-2).jpg|page 2
Image:12-267(HW6-3).jpg|page 3
Image:12-267(HW6-4).jpg|page 4
Image:12-267(HW6-5).jpg|page 5
Image:12-267(HW6-6).jpg|page 6
</gallery>

Latest revision as of 22:53, 9 December 2012

DBN: Classes: 2012-13: 12-267 / Navigation
Additions to this web site no longer count towards good deed points.
# Week of... Notes and Links
1 Sep 10 About This Class. dbnvp Monday: Introduction and the Brachistochrone. dbnvp Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. dbnvp Friday: Some basic techniques: first order linear equations.
2 Sep 17 dbnvp Monday: Separated equations, escape velocities. HW1. dbnvp Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. dbnvp Friday: Reverse engineering separated and exact equations.
3 Sep 24 dbnvp Monday: Solving exact equations, integration factors. HW2. dbnvp Tuesday: Statement of the Fundamental Theorem. Class Photo. dbnvp Friday: Proof of the Fundamental Theorem.
4 Oct 1 dbnvp Monday: Last notes on the fundamental theorem. HW3. dbnvp Tuesday Hour 1: The chain law, examples of variational problems. dbnvp Tuesday Hour 2: Deriving Euler-Lagrange. dbnvp Friday: Reductions of Euler-Lagrange.
5 Oct 8 Monday is thanksgiving. dbnvp Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. dbnvp Friday: More Lagrange multipliers, numerical methods.
6 Oct 15 dbnvp Monday: Euler and improved Euler. dbnvp Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. dbnvp Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
7 Oct 22 dbnvp Monday: Multiple roots, reduction of order, undetermined coefficients. dbnvp Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
8 Oct 29 dbnvp Monday: The basic properties of matrix exponentiation. dbnvp Tuesday: Matrix exponentiation: examples. dbnvp Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
9 Nov 5 dbnvp Monday: Non-homogeneous systems. dbnvp Tuesday: The Catalan numbers, power series, and ODEs. dbnvp Friday: Global existence for linear ODEs, the Wronskian.
10 Nov 12 Monday-Tuesday is UofT November break. HW7. dbnvp Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math].
11 Nov 19 dbnvp Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence. dbnvp Tuesday (class): Airy's equation, Fuchs' theorem. dbnvp Tuesday (tutorial): Regular singular points. HW8. dbnvp Friday: Discussion of regular singular points..
12 Nov 26 dbnvp Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). dbnvp Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. dbnvp Friday: Non-oscillation, Sturm comparison.
13 Dec 3 dbnvp Monday: More Sturm comparisons, changing the independent variable. dbnvp Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
F1 Dec 10
F2 Dec 17 The Final Exam (time, place, style, office hours times)
Register of Good Deeds
12-267-ClassPhoto.jpg
Add your name / see who's in!
12-267-Splash.png

This assignment is due in class on Friday November 9. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.

Task 1. Draw the phase portraits for the following systems, near [math]\displaystyle{ (x,y)=(0,0) }[/math]:

  1. [math]\displaystyle{ \begin{cases} \dot{x}=2x+y \\ \dot{y}=-x+4y \end{cases} }[/math].
  2. [math]\displaystyle{ \begin{cases} \dot{x}=4x-5y \\ \dot{y}=4x-4y \end{cases} }[/math].
  3. [math]\displaystyle{ \begin{cases} \dot{x}=x-2y \\ \dot{y}=-2x+4y \end{cases} }[/math].
  4. [math]\displaystyle{ \begin{cases} \dot{x}=-x+y \\ \dot{y}=-5x+3y \end{cases} }[/math].
  5. [math]\displaystyle{ \begin{cases} \dot{x}=-5x+4y \\ \dot{y}=-8x+7y \end{cases} }[/math].

Task 2. Draw the phase portrait of the system

[math]\displaystyle{ \begin{cases}\dot{x}=17+x-9y+\sin(2-2x-y+xy)\\\dot{y}=7+2x-5y+\cos(x-1)\end{cases} }[/math]

near the point [math]\displaystyle{ (x,y)=(1,2) }[/math].

Task 3. Solve using diagonalization (one solution is enough):

  1. [math]\displaystyle{ v'=\begin{pmatrix} 2 & -1 \\ 3 & -2 \end{pmatrix}v + \begin{pmatrix} e^t \\ t \end{pmatrix} }[/math].
  2. [math]\displaystyle{ v'=\begin{pmatrix} 2 & -5 \\ 1 & -2 \end{pmatrix}v + \begin{pmatrix} -\cos t \\ \sin t \end{pmatrix} }[/math].

Task 4. Assume [math]\displaystyle{ t\gt 0 }[/math]. For the following equation,

[math]\displaystyle{ tv'=\begin{pmatrix} 2 & -1 \\ 3 & -2 \end{pmatrix}v + \begin{pmatrix} 1-t^2 \\ 2t \end{pmatrix} }[/math]

,

it is given that a solution of the homogeneous version is

[math]\displaystyle{ v(t) = c_1\begin{pmatrix}1\\1\end{pmatrix}t + \begin{pmatrix}1\\3\end{pmatrix}t^{-1} }[/math].

Use "fundamental solutions" to find a solution of the full equation.

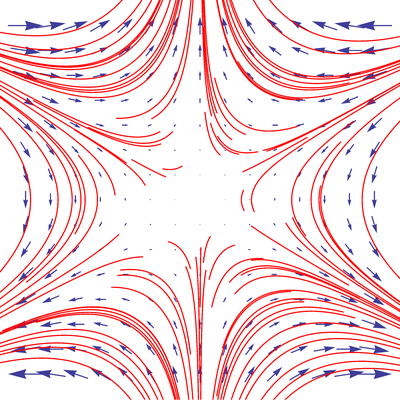
Task 5. (Not for grade). Find a quadratic differential equation whose phase portrait is as below.

12-267-MonkeySaddleFlow.png

Hint. "Monkey Saddle".

Dror's notes above / Student's notes below

Solutions Vsbdthrsh

Solutions to HW6: Dongwoo.kang

  • page 1

    page 1

  • page 2

    page 2

  • page 3

    page 3

  • page 4

    page 4

  • page 5

    page 5

  • page 6

    page 6

Retrieved from "https://drorbn.net/index.php?title=12-267/Homework_Assignment_6&oldid=12788"