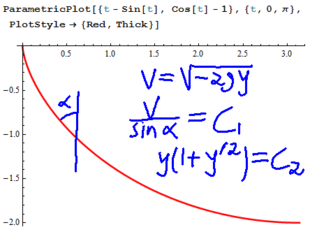12-267/Homework Assignment 2: Difference between revisions
No edit summary |
(Added solution to task 2) |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{12-267/Navigation}} |
{{12-267/Navigation}} |
||
{{In Preparation}} |
|||
This assignment is due at the tutorial on Tuesday October 2. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong. |
This assignment is due at the tutorial on Tuesday October 2. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong. |
||
'''Task 0.''' Identify yourself in the [[12-267/Class Photo|Class Photo]]! |
|||
| ⚫ | |||
| ⚫ | |||
# <math>x^2y^3+x(1+y^2)y'=0</math> (hint: try <math>\mu=x^\alpha y^\beta</math>). |
# <math>x^2y^3+x(1+y^2)y'=0</math> (hint: try <math>\mu=x^\alpha y^\beta</math>). |
||
# <math>dx+(\frac{x}{y}-\sin y)dy=0</math>. |
# <math>dx+(\frac{x}{y}-\sin y)dy=0</math>. |
||
| Line 12: | Line 13: | ||
# <math>\frac{dy}{dx}=\frac{2y+\sqrt{x^2-y^2}}{2x}</math>. |
# <math>\frac{dy}{dx}=\frac{2y+\sqrt{x^2-y^2}}{2x}</math>. |
||
''' |
'''Task 2.''' Let <math>M</math> and <math>N</math> be differentiable functions of <math>x</math> and <math>y</math>. |
||
# Show that if <math>\frac{N_x-M_y}{xM-yN}</math> depends only on <math>xy</math>, then the differential equation <math>Mdx+Ndy=0</math> has an integrating factor of the form <math>\mu(xy)</math>, where <math>\mu</math> is a function of a single variable. |
# Show that if <math>\frac{N_x-M_y}{xM-yN}</math> depends only on <math>xy</math>, then the differential equation <math>Mdx+Ndy=0</math> has an integrating factor of the form <math>\mu(xy)</math>, where <math>\mu</math> is a function of a single variable. |
||
# Find a condition on <math>M</math> and <math>N</math> that would imply that the differential equation <math>Mdx+Ndy=0</math> would have an integrating factor of the form <math>\mu(x+y)</math>, where <math>\mu</math> is a function of a single variable. |
# Find a condition on <math>M</math> and <math>N</math> that would imply that the differential equation <math>Mdx+Ndy=0</math> would have an integrating factor of the form <math>\mu(x+y)</math>, where <math>\mu</math> is a function of a single variable. |
||
''' |
'''Task 3.''' The equation <math>y'+p(x)y=q(x)y^n</math> is called a "Bernoulli Equation". |
||
# Explain why you already know how to solve the Bernoulli equation when <math>n=0</math> and when <math>n=1</math>. |
# Explain why you already know how to solve the Bernoulli equation when <math>n=0</math> and when <math>n=1</math>. |
||
# Show that if <math>n\neq0,1</math>, then the substitution <math>v=y^{1-n}</math> reduces the Bernoulli equation to an equation you already know how to solve. |
# Show that if <math>n\neq0,1</math>, then the substitution <math>v=y^{1-n}</math> reduces the Bernoulli equation to an equation you already know how to solve. |
||
# Solve the equation <math>x^2y'+2xy-y^3=0</math> (for <math>x>0</math>). |
# Solve the equation <math>x^2y'+2xy-y^3=0</math> (for <math>x>0</math>). |
||
''' |
'''Task 4.''' Find an example of a non-differentiable function which is nevertheless Lipschitz. |
||
{{Template:12-267:Dror/Students Divider}} |
|||
'''Solution to Task 2''' --[[User:Twine|Twine]] 18:44, 24 October 2012 (EDT) |
|||
'''Part 1''' |
|||
What we want is an integration factor <math>\mu</math> such that <math>(\mu M)_y = (\mu N)_x</math>. Let <math>xy = z</math> |
|||
When <math>\mu</math> is a function of z, <math>\frac{dv}{dx} = \frac{dv}{dz} \frac{dz}{dx} = \frac{dv}{dz} y</math>. |
|||
Similarly <math>\frac{dv}{dy} = \frac{dv}{dz} x</math>. |
|||
Then we have |
|||
<math>(\mu M)_y = (\mu N)_x</math> |
|||
<math>\iff \mu_{z}xM - \mu_{xy}yN = \mu (N_x - M_y)</math> |
|||
<math>\iff \frac{\mu_{z}}{mu} = \frac{N_x - M_y}{xM - yN}</math> |
|||
If the right hand side depends only on xy, we can get |
|||
<math>\mu (xy) = e^{\int \frac{N_x - M_y}{xM - yN} d(xy)}</math> |
|||
which satisfies the requirements of an integrating factor. |
|||
'''Part 2''' |
|||
As in Part 1, we need <math>(\mu M)_y = (\mu N)_x</math>. Let <math>z = x + y</math> |
|||
When <math>\mu</math> is a function of <math>x + y</math>, <math>\frac{d \mu}{dx} = \frac{d\mu}{dz} \frac{dz}{dx} = \frac{d\mu}{dz}</math>. |
|||
Similarly <math>\frac{d \mu}{dy} = \frac{d\mu}{dz}</math> |
|||
Then we have |
|||
<math>(\mu M)_y = (\mu N)_x</math> |
|||
<math>\iff \frac{\mu_{z}}{\mu} = \frac{N_x - M_y}{M-N}</math> |
|||
If the right hand side of this equation depends only on z (that is, only on (x+y)), then we have |
|||
<math>\mu (x + y) = e^{\int \frac{N_x - M_y}{M - N} d(x + y)}</math> |
|||
which satisfies the requirements of an integrating factor. |
|||
Solution to HW2: [[User:Mathstudent|Mathstudent]] |
|||
<gallery> |
|||
Image:005.jpg|page 1 |
|||
Image:006.jpg|page 2 |
|||
Image:007.jpg|page 3 |
|||
Image:008.jpg|page 4 |
|||
Image:009.jpg|page 5 |
|||
Image:010.jpg|page 6 |
|||
Image:011.jpg|page 7 |
|||
</gallery> |
|||
Latest revision as of 17:44, 24 October 2012
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due at the tutorial on Tuesday October 2. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong.
Task 0. Identify yourself in the Class Photo!
Task 1. Solve the following differential equations:
- (hint: try ).
- .
- .
- (hint: consider trying and for good , ).
- with .
- .
Task 2. Let and be differentiable functions of and .
- Show that if depends only on , then the differential equation has an integrating factor of the form , where is a function of a single variable.
- Find a condition on and that would imply that the differential equation would have an integrating factor of the form , where is a function of a single variable.
Task 3. The equation is called a "Bernoulli Equation".
- Explain why you already know how to solve the Bernoulli equation when and when .
- Show that if , then the substitution reduces the Bernoulli equation to an equation you already know how to solve.
- Solve the equation (for ).
Task 4. Find an example of a non-differentiable function which is nevertheless Lipschitz.
| Dror's notes above / Student's notes below |
Solution to Task 2 --Twine 18:44, 24 October 2012 (EDT)
Part 1
What we want is an integration factor such that . Let
When is a function of z, .
Similarly .
Then we have
If the right hand side depends only on xy, we can get
which satisfies the requirements of an integrating factor.
Part 2
As in Part 1, we need . Let
When is a function of , .
Similarly
Then we have
If the right hand side of this equation depends only on z (that is, only on (x+y)), then we have
which satisfies the requirements of an integrating factor.
Solution to HW2: Mathstudent